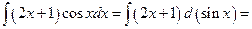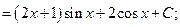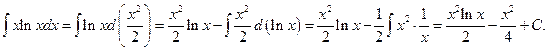Перейдем к формулировке теоремы о замене переменной в неопределенном интеграле, которая часто используется при вычислении интегралов.Здесь имеются в виду два утверждения[1]:
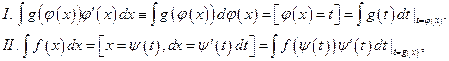
где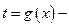 
функция, обратная к функции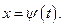 
Теорема 2. а) Пусть выполнены условия: 1) функция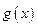 
непрерывна в своей области определения 
б) функция 
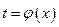непрерывно дифференцируема на множестве 
таком, что
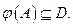Тогда для всех 
имеет место равенство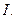 
б) Пусть выполнены условия: 1) функция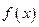 
непрерывна в своей области определения
2) функци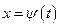и 
и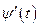 
непрерывны на множестве 
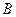таком, что 
3) 
4) функция 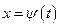имеетна множестве 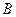обратную функцию 
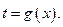Тогда для всех 
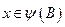имеет место равенство 
Замечание 1. Преобразования в 
часто называют процедурой введения множителя под знак дифференциала. Формулу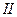 
удобно применять в тех случаях, когда функция 
легче интегрируется, чем исходная функция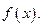 
Её применяют, например, при вычислении интегралов от иррациональностей вида 
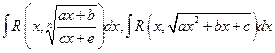(здесь 
рациональная функция). В первом случае делается замена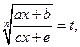 
во втором случае подбирают такую замену 
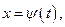чтобы исчезла иррациональность. Например,
= 
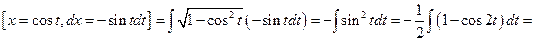
Далее надо вернуться к старой переменной с помощью обратной функции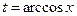 
и получить ответ: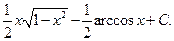 
3. Интегрирования по частям в неопределенном интеграле
При вычислении интегралов часто используется операция интегрирования по частям, законность которой регламентируется следующим утверждением.
Теорема 3. Пусть функции 
непрерывно дифференцируемы на множестве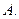 
Тогда на этом множестве справедливо равенство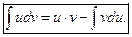 
Доказательство вытекает из цепочкитождеств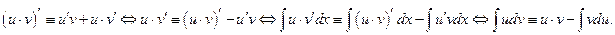 
Замечание 2. Операция интегрирования по частям применяется к интегралам вида
(
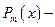многочлен степени 
).
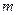При этом в интегралах типа 1 для получения дифференциала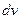 
надо ввести под знак дифференциала трансцендентную функцию 
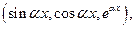а в интегралах типа 2 под знак диффере-
нциала надо ввести многочлен 
Например, 
