1.Конечные точки отрезка попадают в определенную область и им присваивают соответствующий двоичный код
2.Определяется лежит ли отрезок в заданной области:
1. Отрезок в области если логич. ИЛИ концов отрезка равно 0, то отрезок должен быть сохранен.
2. Если логическое И концов отрезка НЕ РАВЕН 0, то отрезок лежит вне области и его нужно отбросить.
3. Если логическое ИЛИ не равно 0, а И равно 0, то отрезок может частично лежать в области отсечения, причем единица логического ИЛИ показывает с какой стороны лежит отрезок от области отсечения.
3.Узнается где пересекаются при отсечении и в случае 3 применяется алгоритм нахождения пересечения отрезка с границей области отсечения.
3. Сечение. В результате сечения получается некоторое пересечение множества точек, двухмерная фигура. Плоскость пересекает трехмерный объект.
S=M^P
M – исходный объект.(трехмерный)
P – секция или плоскость сечения.
S – пересечение плоскости с объектом, т.е двухмерное сечение.
Здесь важно, как задана модель ГО.
В однородных рецепторных моделях задаем объект в некотором пространстве рецепторов.
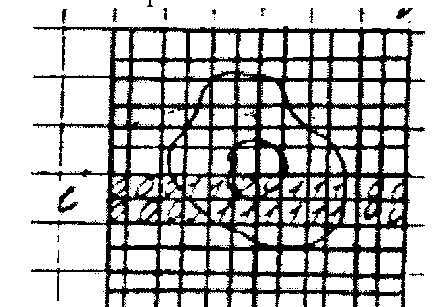
Если плоскость сечения производна, поворачиваем объект так чтобы она стала горизонтальна.
Теперь задача состоит в том, чтобы отличить граничные рецепторы от внутренних.
Сначала нужно сформировать граничные рецепторы.
1. 
Определение правых граничных рецепторов
2.i я строка сдвигается влево на 1 позицию(1-й рецептор)
3.строка инвертируется
4.поразрядное логическое произведение исходной и сдвинутой проинвертированной строки
