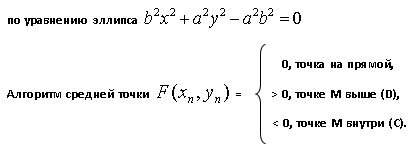Растровые преобразования окружности и эллипса

Существует несколько очень простых, но не эффективных способов преобразования окружностей в растровую форму. Например, рассмотрим для простоты окружность с центром в начале координат. Ее уравнение записывается как x ² + y ² = R ². Решая это уравнение относительно y, получим y = ± .

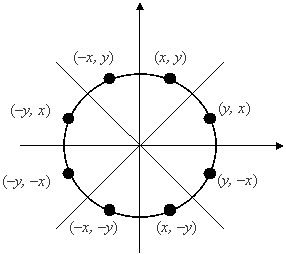Чтобы изобразить четвертую часть окружности, будем изменять x с единичным шагом от 0 до R и на каждом шаге вычислять y. Вторым простым методом растровой развертки окружности является использование вычисление y по формулам x = R cos α, y = R sin α при пошаговом изменении угла α от 0 до 90 градусов.

Для упрощения алгоритма растровой развёртки стандартной окружности можно воспользоваться её симметрией относительно координатных осей и прямых y = ± x; в случае, когда центр окружности не совпадает с началом координат, эти прямые необходимо сдвинуть параллельно так, чтобы они прошли через центр окружности. Тем самым достаточно построить растровое представление для 1/8 части окружности, а все оставшиеся точки получить симметрией.

Рассмотрим участок окружности из второго октанта x Є [0, R / ]. Далее опишем алгоритм Брезенхейма для этого участка окружности.

На каждом шаге алгоритм выбирает точку P_i (x_i, y_i), которая является ближайшей к истинной окружности. Идея алгоритма заключается в выборе ближайшей точки при помощи управляющих переменных, значения которых можно вычислить в пошаговом режиме с использованием небольшого числа сложений, вычитаний и сдвигов.

Рассмотрим небольшой участок сетки пикселов, а также возможные способы (от A до E) прохождения истинной окружности через сетку.

Предположим, что точка P_{i- 1}была выбрана как ближайшая к окружности при x = x_{i- 1}. Теперь найдем, какая из точек (S_i или T_i) расположена ближе к окружности при x = x_{i- 1} + 1.

Заметим, что ошибка при выборе точки P_i (x_i, y_i) была равна D(P_i) = (x_i ² + y_i ²) – R ².

Запишем выражение для ошибок, получаемых при выборе точки S_i или T_i:

D(S_i) = [(x_i-1+ 1)² + (y_i-1)²] – R²;

D(T_i) = [(x_i-1+ 1)² + (y_i-1 – 1)²] – R ².

Если | D(S_i) | ≥ | D(T_i) |, то T_i ближе к реальной окружности, иначе выбирается S_i.

Введем d_i = | D(S_i) | – | D(T_i) |.

T_i будет выбираться при d_i ≥ 0, в противном случае будет устанавливаться S_i.

Опуская алгебраические преобразования, запишем d_i и d_{i+ 1} для разных вариантов выбора точки S_i или T_i. D ₁ = 3 – 2 R.

Если выбирается S_i (когда d_i < 0), то d_{i+ 1} = d_i + 4 x_i-1 + 6.

Если выбирается T_i (когда d_i ≥ 0), то d_{i+ 1} = d_i + 4 (x_{i- 1} – y_{i- 1}) + 10.

Существует модификация алгоритма Брезенхейма для эллипса.