В основе однородной рецепторной модели лежит приближенное представление объекта в поле рецепторов (2-х мерный случай) или пространстве рецепторов (3-х мерный случай).
Рецептор - так называемый чувствительный элемент, который может иметь два состояния: 1 – объект полностью или частично проецируется на него; 0 – нет.
Поле рецепторов – это однородная прямоугольная сетка (матрица) MxN, каждое поле которой - отдельный рецептор.
Входными данными для алгоритмов служат трёхмерные рецепторные матрицы, описывающие объект. Выходные данные – двухмерные рецепторные матрицы, описывающие сечения, проекции, разрезы.
Построим описание области, образующейся в сечении объекта М плоскостью Р. Уравнение плоскости имеет вид Х=хр или Y=yp или Z=zp. Сечением является Qs – слой исходной рецепторной матрицы, однозначно определяемой значением координаты хр, yp или zp. На экране должны высвечиваться только граничные контура сечения, поэтому необходимо выделить граничные рецепторы.
Обозначим qij элементы матрицы Qs; sij – элементы матрицы Sг, описывающей границы сечения, i=1,m, j=1,n.
Выделение правых и левых граничных рецепторов строк Qi определяется как
Выделение верхних и нижних граничных рецепторов определяется как
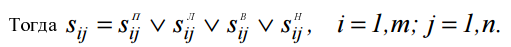
Для построения рецепторного описания штриховки сечения используется матрица строка R размерностью m, в которой через равное число позиций h (шаг штриховки) записаны единицы.
Если обозначить через fi,j элемент матрицы F, содержащий описание штриховки, а через ri,j элемент матрицы R,
то fi,j = qi,j & ri,j.
После построения I-ой строки матрицы F выполняется циклический сдвиг элементов матрицы R на один влево или вправо для формирования направлений штриховки, соответствующим углам 45о и 135о.
Элементы матрицы заштрихованной области сечения определяются как
При реализации макрооперации построения заштрихованной области сечения имеется возможность, используя всё поле процессоров суперЭВМ, обрабатывать строки рецепторной матрицы параллельно.
Для построения проекций и разрезов используется три рецепторных параллелепипеда Q3, R3, и V3 и соответственно три трёхмерные рецепторные матрицы Q, R, и V. Матрица Q содержит описание тела объекта, матрица R – описание ребер, матрица V – очерковых образующих.
Рецепторная матрица S, описывающая только видимые линии проекции, получается с помощью рекуррентных логических операций, выполняемых над всеми слоями параллелепипедов Q3, R3, и V3.
Для удобства организации вычислений Sn можно выполнить следующие преобразования:
Аналогичные преобразования можно выполнить для S. Рецепторная матрица P, описывающая заштрихованный разрез, получается путём объединения рецепторных матриц проекции и заштрихованного сечения.
Чем меньше шаг дискредитации, тем больше рецепторов и тем соответственно больше точность отображения (и тем больше требуется памяти).
Преимущества: Удобство хранения объектов в памяти;Простота выполнения некоторых операций (масштабирования, поворота);Возможность независимо обрабатывать строки и столбцы.
Из недостатков: Большие запросы памяти n*m*p(1000*1000*1000); Необходимость введения параллельного программирования.
10. Матричные модели ГО.
Матричная модель ГО в декартовых координатах этот тип модели используется для описания совокупности линий на поверхности либо в пространстве посредством замены исходной прямой на ломанную линию, проходящую через совокупность точек, принадлежащих исходной линии.
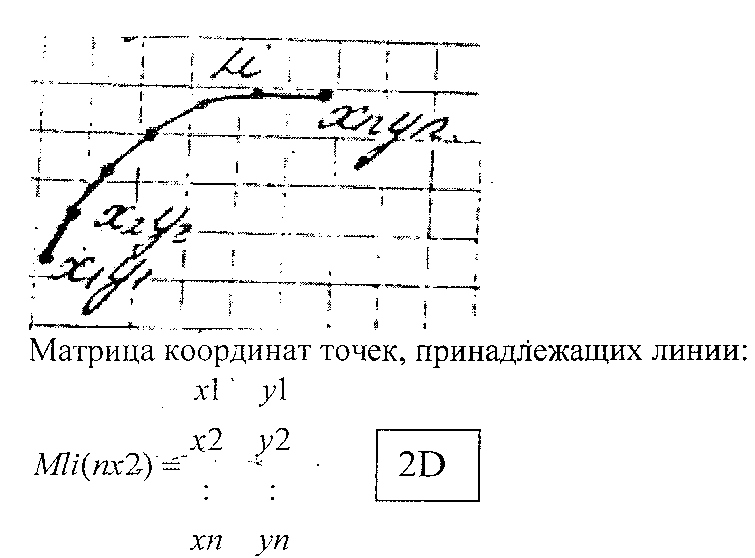Проблема: формализация системных параметров ГО.
, где Мli – это совокупность матриц
