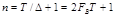Операция замены непрерывной функции последовательностью отсчётов её мгновенных значений называется дискретизацией.
Фундаментальное значение для решения многих задач теории передачи сигналов имеет следующая теорема отсчётов Котельникова:непрерывная функция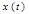 
, не содержащая частот выше граничнойFv, полностью определяется отсчётами мгновенных значений 
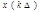в точках, отстоящих друг от друга на интервалы 
. Интервал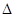 
называется интервалом Котельникова. Эта теорема позволяет представить непрерывную функцию X(T) в виде ряда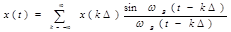 
Процедура восстановления непрерывной функции x(t) по отсчётам её мгновенных значений x(kt) вытекает непосредственно из (6.1): нужно перемножить значения отсчётов x(kt)на соответствующие отсчётные функции (6.2) и просуммировать полученные произведения. Эти операции иллюстрирует рис. 6.4. Спектральная трактовка процесса восстановления x(t) следует из рис. 6.3.
Для полного восстановления необходимо просуммировать бесконечное множество членов ряда (6.1). Однако если функция с ограниченным спектром x(t)рассматривается на конечном интервале Т (рис. 6.4, а), то точное разложение (6.1) можно заменить следующим приближённым разложением:
Конечное число отсчётов п, определяющее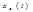 
, равно (при 
) 
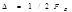