Колебания при угловой модуляции. Рассмотрим особенности обоих видов угловой модуляции: фазовой и частотной. Фазовая модуляция заключается в пропорциональном первичному сигналу x(t) изменении фазы φ переносчика 
, где а — коэффициент пропорциональности. Амплитуда колебания при фазовой модуляции не изменяется, поэтому аналитическое выражение ФМ колебания 
. (8.2)
Максимальное отклонение фазы модулированного колебания от фазы немодулированного колебания M=∆φmax=aX (8.4)
называется индексом модуляции. Индекс модуляции М пропорционален амплитуде Х модулирующего сигнала. Он в такой жестепени характеризует ФМ колебание, как коэффициент модуляции т — AM колебание. Используя (8.4), перепишем ФМ колебание (8.2) как 
. (8.5)
Мгновенная частота ФМ колебания 
. (8.6)
Таким образом, ФМ колебание в разные моменты времени имеет различные мгновенные частоты, отличающиеся от частоты несущего колебания ω0на величину 
, что позволяет рассматривать ФМ колебание как модулированное по частоте. Наибольшее отклонение частоты ω от ω0 называется девиацией частоты ∆ωд= MΩ или ∆fД =MF (8.7)
Частотная модуляция заключается в пропорциональном первичному сигналу x(t) изменении мгновенной частоты переносчика: ω=ω0+ ax(t) (8.8), где а — коэффициент пропорциональности. Аналитическое выражение ЧМ колебания с учетом постоянства амплитуды можно записать в виде:
.
В простейшем случае модуляции гармоническим колебанием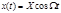 
мгновенная частота 
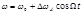, где 
— девиация частоты. Аналитическое выражение этого ЧМ колебания: 
. Слагаемое 
характеризует изменение фазы, получающееся при ЧМ. Это позволяет рассматривать ЧМ колебание, как ФМ колебание с индексом модуляции 
(8.10) и записать его аналогично (8.5): 
. (8.11)
ФМ и ЧМ колебания имеют много общего. Так колебание вида (8.11) может быть результатом как ФМ, так и ЧМ гармоническим первичным сигналом. Кроме того, ФМ и ЧМ характеризуются одними и теми же параметрами (индексом модуляции М и девиацией частоты ∆fД), связанными между собой одинаковыми соотношениями: (8.7) и (8.10).
Спектры колебаний при угловой модуляции. Для определения спектров колебаний при гармонической угловой модуляции является выражение: 
. (8.12)
Угловую модуляцию принято подразделять на узкополосную (М<0,5 рад) и широкополосную (M>0,5рад). Начнем с определения спектра узкополосной угловой модуляции. Полагая M << l, имеем 
, (8.13)
а потому
. (8.14)
Таким образом, спектр узкополосных сигналов угловой модуляции аналогичен спектру простейшего AM колебания. Он содержит компоненты несущей частоты ω0 и двух боковых частот ω0+Ω и ω0−Ω. Параметром, определяющим амплитуды боковых частот, здесь является индекс модуляции М. Ширина спектра узкополосной угловой модуляции такая же, как и при AM: она равна удвоенной частоте модуляции. Несмотря на идентичность спектров, рассматриваемое колебание отличается от AM колебания, что является следствием различия в знаках (т. е. в сдвиге фаз на 180°) компонент нижней боковой частоты. Это означает возможность преобразования AM колебания в узкополосное ФМ колебание поворотом фазы одной из боковых частот на 180°.
При широкополосной угловой модуляции M >> 1 и выражения (8.13) и (8.14) несправедливы. Приходится спектр колебаний определять непосредственно из (8.12). Выражения 
и 
являются периодическими функциями частоты и, а потому они могут быть разложены в ряды Фурье. Первая из этих функций является четной, вторая—нечетной. Таким образом, спектр ЧМ и ФМ колебаний, модулированных гармоническим сигналом, оказывается дискретным, симметричным-относительно ω0 и содержащим бесконечное число боковых частота вида ω0±nΩ с амплитудами An=U0Jn(M). Для М=4 он построен на рис. 1.10.
Соотношения между функциями Бесселя различных порядков, а, следовательно, и между амплитудами различных боковых компонент определяются индексом модуляции М. При некоторых значениях М отдельные компоненты могут исчезнуть (если Jn(M)=0). Это же относится к амплитуде несущей частоты A0=U0J0(M), которая обращается в нуль при М= 2,4; 5,6...
Наличие бесконечно большого числа боковых компонент спектра означает, что теоретически спектр ФМ и ЧМ колебания является бесконечно широким. Однако функция Бесселя Jn(M), начиная с некоторых п<М, быстро убывают с ростом п, что видно на рис. 1.10. Это позволяет ограничить полезный (практический) спектр таких сигналов определенным количеством боковых частот. При ограничении спектра необходимо учитывать влияние двух противоречивых факторов: в более узкой полосе частот ослабляется влияние помех, но одновременно увеличиваются искажения сигнала из-за отсутствия опускаемых составляющих.
Отличие ширины спектра сигналов гармонической угловой модуляции от интервала частот 2∆f д, в пределах которого происходит изменение мгновенной частоты сигнала:
1) теоретическая ширина спектра ∆fчм, фм =∞;
2) практическое ее значение при М <<1 оказывается ∆fчм, фм =2F>>2 ∆f д, а при M>>1 ∆fчм, фм несколько превышает 2∆f д и лишь приближенно считается равной ей.
