Основные свойства нормального закона распределения, применяемые при анализе точности обработки деталей

Ответ: Вероятность соблюдения заданного допуска определяется как отношение площади заключенной между кривой распределения и ординатами (ES, EJ) ко всей площади под кривой распределения.

1. Коэффициент точности

- допуск на контролируемый размер или параметр.

Если , тогда заданная точность (например по чертежу – обеспечивается, так как поле рассеивания случайных величин (например, размеров обрабатываемых деталей) не выходит за пределы регламентированных параметров.

2.Смещение центра группирования (систематическая погрешность) относительно середины поля допуска ( )

где D - номинальное значение контролируемого параметра (например, номинальный размер по чертежу);

ES, EJ - соответственно верхняя и нижняя границы поля допуска.

3.Определение процента % ожидаемого брака.

Вероятность брака по верхнему Pes и нижнему Pej пределам

Для определения табулированных функций Лапласа Ф(Zes) и Ф(Zei) необходимо вычислить значения аргументов.

Значения аргументов Zes, Zej для определения вероятности брака по верхнему ES и нижнему EJ пределам:

, .

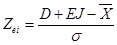Затем по таблицам табулированных функций Лапласа находят значения самих функций Ф(Zes) и Ф(Zej), необходимых для подсчета ожидаемого брака.

В общем случае, применение статистического метода позволяет по данным выборки прогнозировать точность всей обрабатываемой партии деталей, что способствует предсказуемости действующих и вновь проектируемых технологических процессов.

Дата добавления: 2015-02-12; просмотров: 404 | Нарушение авторских прав | Изречения для студентов

Читайте также:

Почему человеку так трудно принимать решения

ПОЧЕМУ ЖЕНЩИНЫ НЕ ОБРАЩАЮТСЯ С ПРОСЬБОЙ

Почему необходим контроль?

Почему трудно полюбить зелень?

Рекомендуемый контект:

Поиск на сайте:

© 2015-2020 lektsii.org - Контакты - Последнее добавление