Молекулярная физика

Открытия в области физики молекул и газов позволили ученым убедиться экспериментально в том, что все вещества, в том числе и живые организмы, состоят из мелких и неделимых частиц – атомов. Человек осознал и научился использовать такие понятия как масса, объем, давление и температура. Были созданы устройства, позволяющие их измерять. Между ними были установлены закономерные связи, открыты законы газов. Исследования в области физики молекул позволили сделать важный шаг к развитию химии и биохимии, статистической физики.

Описание состояния различных веществ, например газа, можно осуществлять с помощью различных теоретических подходов.

Микроскопическое описание рассматривает детали движения и взаимодействия молекул в рамках кинетической теории и статистической механики7. Пример микроскопического описания – это использование законов механики для описания движения и столкновения между собой молекул

или атомов. Составленные, таким образом системы уравнений позволяют объяснить, например, возникновение давления газа на стенки сосуда или получить уравнение газового состояния с точки зрения микроскопического описания.

Макроскопическое описание оперирует с измеряемыми физическими величинами: массой, объемом, давлением, температурой. Например, состояние газа в сосуде описывается тремя переменными: V (объем), P (давление), T (температура). В квартире воздух, заполняющий ее, также характеризу-

 

7 Статистическая механика – это раздел физики, рассматривающий закономерности движения большого числа частиц.

ется объемом, температурой и давлением. Такие величины называют параметрами состояния. Изучением процессов с помощью макроскопических величин занимается термодинамика.

Кинетической называют теорию, согласно которой вещество состоит из атомов, совершающих непрерывное хаотическое движение.

Строение вещества. Идея о существовании мельчайших неделимых частиц принадлежит древнегреческому философу Демокриту8. Эти частицы он назвал атомами (от древнегреческого слова атомос – «неделимый»).

Экспериментальные подтверждения справедливости атомной теории были получены лишь в XVIII в. Вполне естественно объяснение таких характеристик веществ как проницаемость, сжимаемость, растворимость тем, что вещество не является сплошным, но состоит из отдельных частиц, между которыми есть промежутки. Притяжение молекул и атомов является причиной существования твердых и жидких тел. Однако при приближении атомов друг к другу между ними возникают силы отталкивания. Таким образом, средние расстояния между атомами остаются примерно одинаковыми. Видно, что сжать воду или какое-либо твердое тело практически невозможно.

Явление диффузии – явление самопроизвольного взаимного проникновения веществ (рис. 2.1) – является подтверждением того, что атомы и молекулы вещества находятся в постоянном и беспорядочном движении. Диффузия имеет место в газах, жидкостях и твердых телах. Это, например, запахи при диффузии в газах, самопроизвольное смешивание различных слоев жидкостей.

Ярким экспериментальным доказательством атомного строения вещества явились опыты английского ботаника Броуна в 1827 г. (рис. 2.2).

 

8 Греческий философ Демокрит жил ок. 460–370 гг. до н.э. Он был учеником и последователем греческих философов Анаксагора (500–428 гг. до н.э.), высказавшем мысль о существовании «неразрушимых элементов» и Левкиппа (V в. до н.э.), подхватившим идеи атомистики.

 

 

Он обнаружил в пыльцы непрерывно

 

микроскоп, что крупинки цветочной хаотически движутся. Их беспорядоч-

ное движение объяснялось столкновениями с молекулами воды. Интенсивность такого движения обусловлена соотношением массы частиц и молекул воды. Массивные частицы не испытывали хаотического движения. Мелкие – при столкновениях с молекулами воды сильно изменяют направление своего движения. Количественная теория броуновского движения была разработана Эйнштейном в 1905 г. Он оценил на основе экспериментальных данных размер и массу атомов и

молекул, которые составили около 10–10 м

и 10–27 кг.

 

 

 

Рис 2.1. Диффузия капли чернил

в воде

 

Рис. 2.2. Движение броуновской частицы

Температура. Представление о горячем и холодном мы связываем с понятием температуры. Температура влияет на многие свойства веществ: плотность, объем, давление, электрическое сопротивление, вязкость, цвет и т.д. Уже в древние времена ученые пытались и не безуспешно теплом лечить различные недуги.

С точки зрения микроскопической теории с ростом тем-

пературы

атомы вещества колеблются вокруг своего поло-

жения равновесия с большей амплитудой

(пропорционально

ее квадрату). С понижением температуры молекулы двигаются с меньшей средней скоростью. Поэтому мы ощущаем холод.

 

Измерение температуры осуществляется термометром. Первый такой прибор был изобретен в XVII в. Галилеем, в нем ученый использовал расширение газа. Газовый термометр показан на рис. 2.3. Термометр работает при постоянном объеме для разных типов газов.

 

Рис. 2.3. Газовый термометр

Тепловое расширение. Изменение температуры тела приводит к линейному и объемному расширению тел. Нагреваясь, тела увеличивают свои линейные размеры и объем, а охлаждаясь, – уменьшают. Эта зависимость в широком интервале температур носит линейный характер. Линейное раcширение тел определяется соотношением

l = l 0(1 + αt), (2.1.1)

где α – коэффициент линейного расширения вещества, l 0 –

длина при температуре 0ºС.

Физическая причина возникновения линейного и объемного расширения тел заключается в том, что с ростом температуры увеличивается амплитуда колебаний атомов в веществе друг относительно друга. Поэтому среднее расстояние между ними возрастает. Линейное и объемное расширение тел – по смыслу это один и тот же эффект, поскольку расстояние между атомами увеличивается по трем координатам. В случае, когда поперечные размеры тела малы, то учитывается их линейное расширение, а расширением тел в попереч-

ном направлении можно пренебречь. В случае, когда размеры тела в трех измерениях сравнимы по величине, рассматривают объемное расширение.

При строительстве железных дорог необходимо учитывать только линейное расширение рельсов, поскольку их линейные размеры много больше поперечных. Между рельсами предусматривается зазор 1–2 см. Летом рельсы могут разогреваться до температуры 50ºС, а зимой их температура может достигать –50ºС. Коэффициент линейного расширения

стали ~10–5, что при длине рельса 20 м составит увеличение

длины на

~2 см. При отсутствии зазора

рельсы могут под-

няться, что приведет к аварии на железной дороге.

Объемное расширение тел определяется соотношением

V = V 0(1 + βt),

(2.1.2)

где β – коэффициент объемного расширения вещества, V 0–

объем системы при температуре 0ºС.

Коэффициенты α и β связаны соотношением

β ≈ 3 α.

(2.1.3)

Коэффициенты линейного и объемного расширения измеряются в обратных градусах Цельсия град–1. Их величины для

жидкостей

составляют 10–3–10–4 град–1,

а для твердых ве-

ществ 10–5–10–6 град–1. Явление теплового расширения тел положено в основу работы различных термометров, где в качестве термометрической величины выступает высота столбика из жидкости, газа или твердого тела (рис. 2.4).

.

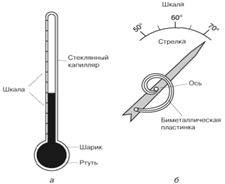
Рис. 2.4. Ртутный термометр (а); биметаллический термометр (б)

Законы идеального газа. Идеальным называют газ, молекулы которого представляют собой материальные точки, все столкновения которых являются абсолютно упругими, и потенциальной энергии взаимодействия между ними нет. Поэтому в модели идеального газа происходит хаотическое движение материальных точек, которые взаимодействуют между собой только в результате упругого столкновения.

Описание состояния системы заключается в установлении связи между макроскопическими параметрами (V, P, Т, m). Когда один или два макропараметра системы постоянны, зависимости носят название изопроцессов.

Процесс, при котором давление и объем газа меняются,

m = const, T = const, называется изотермическим:

PV = const, m = const, T = const. (2.1.4)

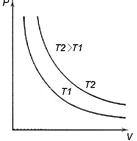
Этот закон был открыт Бойлем и Мариоттом (рис. 2.5, а) одновременно и получил название закона Бойля–Мариотта 9.

Экспериментально были установлены линейные зависимости объема и давления идеального газа от температуры V

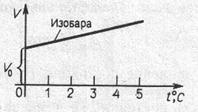
= V (T) и P = P (Т), которые получили название законов соответственно Шарля (рис. 2.5, б) и Гей-Люсcака (рис. 2.5, в):

P = P 0(1 + αt),

или

Р 1= Т 1, m = const, V = const (2.1.5)

Р 2 Т 2

– закон Гей-Люссака10

 

 

9 Впервые мысль о постоянстве произведения давления на объем была высказана английским физиком Р. Тоунли. Такие же исследования проводил врач Г.Пауэр. Английский физик Роберт Бойль провел исследования в широких пределах и опубликовал результаты в 1662 г., а независимо от него французский физик Э. Мариотт опубликовал свои исследования в 1676 г.

10 Гипотеза о пропорциональности давления температуре была высказана французским физиком Г.Амонтоном в 1702 г., а 100 лет

спустя французский физик Ж.Л. Гей-Люссак получил математическое выражение этого закона. Им же был открыт в 1802 г. и закон пропорциональности объема газа температуре. Однако первым его 45

 

или

 

V = V 0(1 + αt),

 

V 1 = T 1, m = const, P = const (2.1.6)

V 2 T 2

– закон Шарля, где α – коэффициент объемного расширения или увеличения давления α = 1/273 град–1.

 

 

а б

в

Рис. 2.5. Законы идеального газа: а) закон Бойля–Мариотта

(изотермы для T 2 > T 1); б) закон Шарля; в) закон Гей-Люсака

Уравнение состояния идеального газа. Из установленных экспериментально законов изменения состояния идеального газа (2.1.4)–(2.1.6) следует

PV = Р 0 V 0 = R = const, (2.1.7)

T T 0

где R = 8.31 Дж/моль × К называют универсальной газовой постоянной.

открыл другой французский физик – Ж. Шарль, не опубликовавший результаты своих экспериментов.

Упомянутые законы являются частными случаями более общего уравнения газового состояния, которое называют уравнением Клапейрона.

Уравнение Клапейрона–Менделеева11для произвольной

массы идеального газа учитывает также и количество молей газа:

PV = mRT = NkT, (2.1.8)

m

где m / μ = N / N A= ν – число молей газа, k = R / N A=1.38·10–23

Дж/К – постоянная Больцмана.

Законы Бойля–Мориотта, Гей-Люсакка, Шарля и уравнение газового состояния являются частными случаями уравнения Клапейрона–Менделеева.

Постоянство величины R для разных газов представляет гениальное отражение простоты природы. Итальянский ученый Амедео Авогадро12(1776–1856) установил, что равные объемы газов при равных давлениях и температурах имеют одинаковое число молекул N. Это видно из уравнения газо-

вого состояния, переписанного в виде

N = PV, (2.1.9)

kT

где k – постоянная Больцмана. При нормальных условиях газа, когда Т 0= 0ºС, Р 0= 1 атм, V 0= 22.4 м3 для любого вида газа количество молекул, называемое числом Авогадро, составляет

N A= 6.02 · 1023моль–1. (2.1.10)

Закон Дальтона. Если в пустой объем впустить какойлибо газ, то он займет весь объем. Если объем заполнить воздухом, то давление будет равно давлению трех состав-

 

 

11Это уравнение впервые было получено в 1874 г. русским ученым Д.И. Менделеевым на основе обобщения результатов исследований французского физика Б.П. Клайперона и записано в такой форме.

12 Гипотеза впервые была им сформулирована в 1811 г. В закон она превратилась в 1863 г. после того, как была доказана Клаузиусом.

ляющих его газов (кислорода, азота и углекислого газа), т.е. давление смеси химически не взаимодействующих идеальных газов равно сумме парциальных давлений этих газов (закон Дальтона):

Р = Р 1 + Р 2 + Р 3 + … + Рn, (2.1.11)

причем каждый газ в смеси создает парциальное давление, пропорциональное его молекулярной концентрации:

i

P = miRT, (2.1.12)

miV

где mi и μi – масса и молярная масса i -го компонента газовой смеси.

При нормальных условиях, т.е. при температуре 0ª (273 К) и давлении 101.3 кПа, объем Vµ (молярный объем) равен 0.022414 м3/ моль.

Основное уравнение молекулярно-кинетической теории идеального газа устанавливает связь между микроскопическим и макроскопическим подходами при описании состояния газа. Фактически оно устанавливает те же закономерности, что уравнения газового состояния и уравнение Клапейрона–Менделеева.

Уравнение молекулярно-кинетической теории имеет вид

P = 1 nmv 2, (2.1.13)

или

 

 

mv 2

P = 2 nW

3 к

 

, (2.1.14)

где Wк =

– кинетическая энергия молекул идеального

газа,

n = N

V

– число молекул в единице объема. Это уравне-

ние связывает между собой макроскопический параметр давление P с массой молекул и их среднеквадратичной скоростью v 2.

Сравнивая (2.1.9) и (2.1.14), видим, что средняя кинетическая энергия молекулы и температура связаны соотношением

 

W = 1 m v 2

к 2

= 3 kT. (2.1.15)

Вдоль каждой из пространственных осей молекулы имеют одинаковую среднюю кинетическую энергию:

1 2 1

Wi = m v i

= kT. (2.1.16) 2

Таким образом, основное уравнение молекулярно-кинетической теории устанавливает связь между средней кинетической энергией молекул (микропараметр) и температурой газа (макропараметр).

Распределение Максвелла молекул по скоростям. В экспериментах по проверке молекулярно-кинетической теории, проведенных Штерном в 1920 г., была получена средняя скорость молекул, которая составила 650 м/c.

Однако при этом было замечено, что плотность распределения молекул по скоростям оказывалась неравномерной, что можно было объяснить различным количеством молекул, имеющих разные скорости. В последующих экспериментах была получена зависимость числа молекул от их скорости.

В газе, находящемся в состоянии равновесия, при данной температуре устанавливается некоторое стационарное состояние, не меняющееся со временем распределение молекул по скоростям. Это распределение описывается функцией f(r) – функцией распределения молекул по скоростям, которая определяет относительное число молекул, скорости которых лежат в интервале от r до r + dr, т.е.

dN(r)= f(r)dr. (2.1.17)

N

Аналитическое выражение, описывающее распределение молекул по скоростям было получено выдающимся английским физиком Джеймсом Максвеллом:

3 mv 2

f (V) = 4 p v 2 N (

m

2 p kT

)2 e -2 kT. (2.1.18)

Кривые распределения молекул по скоростям начинаются в начале координат, асимптотически приближаются к оси абсцисс при бесконечно больших скоростях (рис. 2.6). Слева от максимума кривые идут круче, чем справа. То что кривая

распределения начинается в начале координат, означает, что неподвижных молекул в газе нет. Из того, что кривая асим-

птотически

приближается к оси абсцисс при бесконечно

больших скоростях, следует, что молекул с очень большими скоростями мало. Для того чтобы молекула могла приобрести при столкновениях очень большую скорость, ей необходимо получить подряд много таких столкновений, при кото-

рых она получает энергию, и

ни одного

столкновения, при

котором она ее теряет. А такая ситуация маловероятна.

 

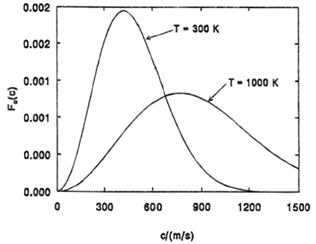
Рис. 2.6. Распределения Максвелла молекул газа по скоростям для различных температур

Уравнение Ван-дер-Ваальса. Экспериментальные ис-

следования

показали, что уравнение Бойля–Мариотта для

реальных газов выполняется не совсем точно. Причиной этого является действие между молекулами сил как притяжения, так и отталкивания. Кроме того, молекулы лишь в идеальном приближении можно считать упругими и имеющими пренеб-

режимо малые размеры. Силы

межмолекулярного

взаимо-

действия очень сильно зависят от расстояния между молекулами. С ростом этого расстояния силы отталкивания убывают быстрее, чем силы притяжения, а при уменьшении этого расстояния возрастают быстрее сил притяжения.

 

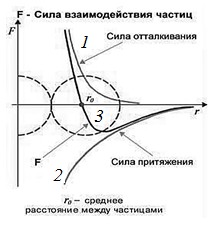
Рис. 2.7. Сила взаимодействия между молекулами; линия 3 – суммарное действие сил притяжения и отталкивания

Силы межмолекулярного взаимодействия – короткодействующие – они проявляются на расстояниях менее 10–9м. Силы отталкивания и притяжения хорошо описываются фун-

кцией f ~ 1: сила отталкивания f

~ 1 (рис. 2.7, верхняя

rn от

r12

кривая), сила притяжения – fприт ~ r7 (рис. 2.7, нижняя кривая). Разная степень зависимости этих сил от расстояния между молекулами приводит к появлению положения устойчивого равновесия (рис. 2.7, красная линия) и минимальной потенциальной энергии взаимодействия молекул. Положение устойчивого равновесия определяется равенством сил притяжения и отталкивания. Колебания молекул происходят вокруг положения устойчивого равновесия. Минимальная энергия взаимодействия двух молекул соответствует ее значению в положении равновесия, вокруг которого происходят их колебания (рис. 2.7).

В реальном газе уравнение Менделеева–Клапейрона имеет несколько другой вид. Это обусловлено тем, что давление реального газа на стенку оказывается ниже. Также меньше будет и объем пространства, в котором двигаются молекулы, поскольку они имеют реальный размер.

 

Физические причины уменьшения давления в реальных газах заключаются в следующем. На молекулу, находящуюся в поверхностном слое газа, как и при поверхностном натяжении жидкости, действует сила, направленная вовнутрь. Молекулы, двигающиеся к стенке сосуда, замедляются под дей-

ствием этой силы. Уравнение

Клайперона–Менделеева ре-

ального газа было скорректировано Ван-дер-Ваальсом:

(P +

a

 

V

2

моля

 

 

)(V

моля

- b) = RT.

(2.1.19)

Изотермы реальных газов представлены на рис. 2.7. При вы-

соких температурах

изотерма реального газа мало от-

личается от изотермы идеального газа (верхняя линия на рис. 2.7, а). При некоторой температуре – критической температуре – на изотерме появляется точка перегиба K – крити-

ческая точка. Соответствующие этой точке объем

и давле-

ние называются критическими. Изотерма при называется критической изотермой. При критической температуре теряется различие между жидкой и газообразной фазой вещества.

 

 

а б

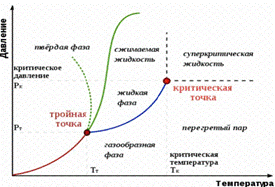
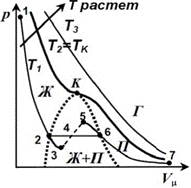
Рис. 2.8. Изотермы Ван-дер-Ваальса (а);

фазовая диаграмма вещества (б)

 

 

При T € Tкуравнению Ван-дер-Ваальса соответствует кривая 1–2–3–4–5–6–7. Участок 6–7 соответствует газообразной фазе, участок 1–2 – жидкой фазе. Фаза вещества – макроскопическое физически однородное равновесное состояние вещества. Например, вода может находиться в парообразной (П), жидкой (Ж) или твердой фазе. На участке 2–3– 4–5–6 соответствует равновесному состоянию жидкости и пара (Ж + П). В этом случае пар называется насыщенным, т.е. число молекул жидкости, покидающих поверхность пара равно число молекул пара, возвращающихся обратно в жидкость. Ненасыщенный пар – пар, в котором число вылетающих молекул превышает число возвращающихся.

Для наглядного изображения фазовых превращений используется диаграмма состояния, на которой в координатах (PT) задается зависимость между температурой фазового перехода и давлением в виде кривых испарения (КИ), плавления (КП) и сублимации (КС), разделяющих поле диаграммы на три области, соответствующие условиям существования твердой (ТТ), жидкой (Ж) и газообразной (Г) фаз. Фазовый переход – изменение состояния вещества, связанное с переходом из одной фазы у другой.

Кривые рис. 2.8, б называются кривыми фазового равновесия, каждая точка на них соответствует условиям равновесия двух сосуществующих фаз. Диаграмма состояния позволяет судить, в каком состоянии находится данное вещество при определенных макропараметрах P и T, а также какие фазовые переходы будут происходить в том или ином процессе. Тройной точкой называется точка, в которой пересекаются кривые фазового равновесия и которая, следовательно, определяет условия одновременного равновесного сосуществования трех фаз вещества. Тройная точка воды соответствует температуре 273.16 К (или 0.01ºC) и является основной реперной точкой для построения термодинамической темпе-

ратурной шкалы.