В этом примере упругий стержень, закрепленный с одной стороны, изгибается магнитами, которые помещены вблизи его свободного конца. Магнитные силы делают неустойчивым прямое, неизогнутое состояние стержня и создают несколько положений равновесия, одно из которых показано на рисунке 1.82.
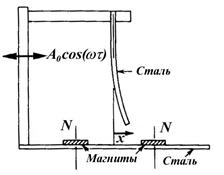
Рисунок 1.82 - Упругий стальной стержень, изогнутый магнитными массовыми силами и прикрепленный к периодически движущемуся основанию
В экспериментах с помощью четырех магнитов создавалось до четырех положений устойчивого равновесия. После того как такой изгиб создан, система аналогична частице в потенциале из двух или более ям.
Устройство помещается на вибростенд и колеблется с постоянной амплитудой и частотой. При слабых колебаниях стержень остается вблизи одного из положений равновесия. С ростом амплитуды стержень может выскочить из потенциальной ямы и начинаются хаотические движения, при которых стержень переходит из одной ямы в другую
Для описания этой системы используется приближение со многими модами уравнения, в котором учтены нелинейные магнитные силы, действующие на свободный конец стержня.
Для стержня с затуханием, закрепленного с одной стороны, хорошие результаты дает приближение с одной модой. Соответствующее уравнение можно записать в виде системы трех уравнений первого порядка.
Обратите внимание, что здесь переменная 
является безразмерной амплитудой гармоники, а не расстоянием вдоль стержня:
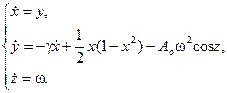
Эта задача аналогична задаче о частице в паре потенциальных ям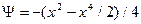 
. Отображение Пуанкаре имеет вид, характерный для двумерных точечных отображений.
В типичных случаях эксперименты не обнаружили удвоений периода перед переходом к хаотическому движению. Предвестниками хаоса часто оказывались нечетные субгармоники.
Видоизменением этого эксперимента является перевернутый маятник с пружиной. Если пружина слабая, то, как и в задачах с двумя потенциальными ямами, перевернутый маятник имеет два положения устойчивого равновесия.
