Было проведено много экспериментов с хаотическими колебаниями упругих стержней. Исследованы проблемы двух типов.
В задачах одного класса уравнение в частных производных, описывающее движение стержня, линейно, но не линейны массовые силы или граничные условия. В других задачах движения достаточно сильны, чтобы в уравнениях движения стали существенными нелинейные члены.
При малых изгибах и отклонениях уравнение движения упругого
,
где 
– поперечное смещение стержня, 
– коэффициент упругой жесткости, 
– масса на единицу длины.
Правая часть уравнения описывает распределенные массовые силы или внутреннее затухание. Во многих опытах, для создания нелинейных массовых сил использовались постоянные магниты.
Когда смещение и наклон оси стержня велики, горизонтальное и вертикальное смещение и наклон характеризуются переменными 
, связанными соотношениями
.
где 
– длина, измеряемая вдоль деформированного стержня (см. рисунок).
Рисунок 1.81 - Плоская деформация упругого стержня
Уравнения сохранения импульса приобретают вид
,
где
.
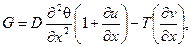
В этих уравнениях 
– компоненты массовой силы, а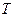 
– осевая сила, создающая напряжения в стержне. Нелинейные члены отличаются от характерных для механики жидкостей тем, что сюда не входят переносные, или кинематические, нелинейности. Локальная зависимость напряжений от деформации линейна. Нелинейные члены возникают из-за изменения геометрической формы и называются геометрическими нелинейностями.
