Большинство дифференциальных уравнений, моделирующих физические системы, нельзя решить аналитически. Исключением из этого правила является класс задач с импульсными силами, крутящими моментами или напряжениями. В обсуждаемом здесь примере рассматривается ротатор с моментом инерции 
и затуханием 
, на который действует как постоянный крутящий момент 
, так и периодическая серия импульсных толчков.
Уравнение движения, описывающее изменение углового момента ротатора
, где 
.
Выражение 
обозначает дельта-функцию, которая равна нулю повсюду, кроме значений 
, и площадь под которой равна единице. В промежутки времени 
, где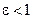 
, изменение углового момента описывается соотношением
.
Если ротатор подталкивается вертикальной силой, то импульсный крутящий момент пропорционален 
. При 
уравнение имеет стационарное решение 
, 
. Чтобы получить отображение Пуанкаре, выберем сечение непосредственно перед каждым импульсом. Итак, определим 
, 
. Чтобы связать 
с 
, необходимо решить линейное дифференциальное уравнение для периода между импульсами и использовать условие скачка углового момента в момент импульса. Между импульсами скорость вращения ведет себя следующим образом (рисунок 1.79):
.
Рисунок 1.79 - Ротатор с вязким затуханием и периодическим крутящим моментом
С помощью этой процедуры можно получить следующее точное отображение Пуанкаре для рассматриваемой системы:
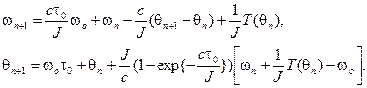
Эти уравнения были впервые получены русским физиком Заславским при изучении нелинейного взаимодействия двух осцилляторов. В рассматриваемом механическом аналоге этой задачи величина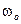 
у аналогична частоте отдельного осциллятора.Это двумерное отображение часто делают безразмерным посредством соотношений
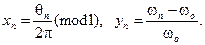
Тогда при и 
уравнения принимают вид
где фигурные скобки {} обозначают, что берется только дробная часть выражения (т.е. mod 1 или 
). Кроме того, здесь введены обозначения 
, 
и 
. Величиной 
измеряется отклонение скорости вращения от невозмущенного равновесного значения 
(рисунок 1.80)
Рисунок 1.80 - Странный аттрактор отображения Заславского для подталкиваемого ротатора
Можно показать, что при малых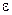 
эта система двух разностных уравнений имеет хаотические решения только при выполнении следующих условий: 
.
На рисунке показано типичное решение, полученное для значений параметров 
и 
.
