Инженерам часто приходится отыскивать источник нежелательных колебаний, возникающих в физических системах. Возможность классификации природы колебаний может подсказать пути контроля над ними. Например, если система считается линейной, то сильные периодические колебания могут возникать из-за резонансных эффектов.
Однако если система нелинейная, то периодические колебания могут возбуждаться из-за существования предельного цикла, который в свою очередь можно связать с динамической неустойчивостью системы.
Для выявления непериодических, или хаотических, движений предлагаются следующие действия:
- выявите нелинейные элементы системы;
- проверьте, присутствуют ли источники случайных внешних воздействий;
- рассмотрите временную эволюцию измеряемого сигнала;
- поинтересуйтесь эволюцией на фазовой плоскости;
- исследуйте фурье-спектр сигнала;
- получите отображение Пуанкаре сигнала;
- измените параметры системы (пути к хаосу).
Ниже мы разберем эти пункты представленного списка и опишем признаки хаотических колебаний. Чтобы конкретизировать обсуждение, для иллюстрации признаков хаотической динамики выбраны колебания изогнутого стержня (задача с парой потенциальных ям).
Для диагностики хаотических колебаний необходимо ясное определение такого движения. Однако по мере того, как новые исследования раскрывают новые сложности нелинейной динамики, строгие определения оказываются ограниченными определенными классами математических задач. Это создает трудности для экспериментатора, поскольку его цель – выяснить, какая математическая модель наилучшим образом описывает данные. Поэтому на данном этапе развития этой науки мы используем одновременно ряд диагностических критериев и рассматриваем различные классы хаотических движений. Экспериментаторам рекомендуется применять по два и более тестов, чтобы получить адекватную картину хаоса.
Возможны следующие классы движений в нелинейных детерминированных системах.
Предсказуемое регулярное движение: периодические колебания, квазипериодическое движение; нечувствительно к изменениям параметров и начальных условий.
Непредсказуемое регулярное движение: множественные регулярные аттракторы (допустим более чем один тип периодического движения); длительное движение чувствительно к начальным условиям.
Переходный хаос: движения, которые кажутся хаотическими и имеют характерные для странного аттрактора свойства (обнаруживаемые по отображению Пуанкаре), но в конце концов вырождаются в регулярное движение.
Перемежаемый хаос: периоды регулярного движения, прерываемого переходными вспышками хаотического движения; длительность периодов регулярного движения непредсказуема.
Ограниченный, или узкополосный, хаос: хаотические движения, орбиты которых проходят в фазовом пространстве вблизи от орбит некоторых периодических или регулярных движений; их спектры часто обнаруживают небольшое или ограниченное расширение определенных частотных компонент.
Слабый крупномасштабный или широкополосный хаос: динамические процессы можно охарактеризовать с помощью орбит в фазовом пространстве малого числа измерений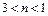 
(от 1 до 3 мод в механических системах). Обычно удается измерить фрактальную размерность, которая оказывается меньшей 7; хаотические орбиты охватывают обширные области фазового пространства; спектры состоят из широкого набора частот, особенно меньших частоты возбуждения (если последнее присутствует)
Сильный крупномасштабный хаос: динамические свойства можно описать только в фазовом пространстве очень большого числа измерений; присутствует большое число существенных степеней свободы; трудно получить надежную оценку фрактальной размерности; до сих пор не существует динамической теории явления.
Чтобы помочь разобраться в растущем числе определений и классов хаотических движений, мы перечислим наиболее распространенные признаки без математических формул, но с указанием в скобках наиболее приемлемого диагностического метода.
