Для вычисления финальных вероятностей составим по графу состояний марковской цепи, изображенной на рис. 2.34, систему уравнений. Так как коэффициент готовности будет рассчитываться для установившегося режима, то систему дифференциальных уравнений сразу преобразуем в систему алгебраических уравнений (2.108):
 ,
,
 ,
,
 ,
,


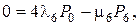




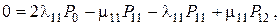


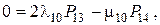

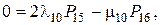





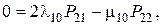



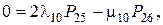



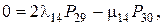

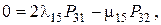



Решая систему уравнений методом подстановки, найдем финальные вероятности в выражении для коэффициента готовности:



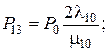


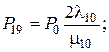

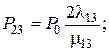



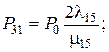

Поскольку коэффициент готовности – это сумма вероятностей пребывания системы в работоспособных состояниях,
K г = Р 0 + Р 9 + Р 11 + Р 13 + Р 15 + Р 17 + Р 19 + Р 21 + Р 23 + Р 25 +
+ Р 27 + Р 29 + Р 31 + Р 33 = 0,9996. 
В данном примере еще раз использовалась методика расчета надежности сложных технических систем, изложенная в подразд. 2.3.2. В отличие от предыдущих примеров (2.9–2.12), исследуемая система состояла из достаточно большого количества блоков, что привело к необходимости разработать эмпирические правила по усечению графа переходов системы. Однако структура СТС являлась регулярной, и построение структурно-логической схемы надежности системы не представляло особых сложностей. Рассмотрим еще один пример реальной системы, в которой основную трудность представляет именно построение структурно-логической схемы надежности.
Пример 2.14. Проектная оценка надежности автоматизированной информационно-измерительной системы (АИИС) «Алтайэнерго».
Структурная схема АИИС «Алтайэнерго» приведена на рис. 2.35. АИИС предназначена для измерения параметров на указанных подстанциях и передаче их в ОАО «Алтайэнерго» г. Барнаула через корпоративную сеть передачи данных. Если корпоративная сеть или ее блоки отказали, то передавать информацию можно через сотовую сеть связи стандарта GSM. Для такой системы с повышенной надежностью функций передачи данных следует определить понятие отказа. В нашем случае отказом АИИС КУЭ будем считать невозможность выполнения системой функций в полном объеме.
 |
Рис. 2.35. Структурная схема АИИС «Алтайэнерго»






