Ответ по второму способу: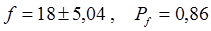 
.
Интервальная оценка погрешности по второму способу уже, чем по первому способу.
12.3. ПРИМЕР ПРАКТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ
При измерениях с многократными наблюдениями обработка результата проводится по-разному в зависимости от числа серий наблюдений, условий и числа измерений в каждой серии, значимости систематических погрешностей и ряда других факторов. В простейшем случае, когда выполнена одна серия наблюдений с числом измерений n <12, ограничиваются вычислением среднего арифметического результата наблюдений (математического ожидания) и оценки его среднеквадратического отклонения (СКО).
В общем случае порядок обработки результатов прямых измерений с многократными наблюдениями регламентирует ГОСТ 8.207-76. При этом необходимо выполнить следующие операции:
1. Исключение систематических погрешностей.
2. Исключение грубых погрешностей (промахов) из результатов наблюдений.
3. Вычисление среднего арифметического исправленных результатов наблюдений, которое принимается за результат измерения.
4. Вычисление оценки СКО результата наблюдения.
5. Вычисление оценки CКО результата измерения.
6. Проверка гипотезы о том, что результаты наблюдений принадлежат нормальному закону распределения.
7. Вычисление доверительных границ случайной погрешности (случайной составляющей погрешности) результата измерения.
8. Вычисление границы неисключенной систематической погрешности (неисключенных остатков систематической погрешности) результата измерения.
9. Вычисление доверительных границ погрешности результата измерения.
На практике наиболее важным и распространенным является случай, когда нет необходимости оценки неисключенных остатков систематических погрешностей.
Рассмотрим для данного случая порядок обработки результатов измерений на конкретном примере (например, на измерении напряжения U на выходе электронного узла).
Покажем пример обработки результатов прямых измерений с многократными наблюдениями. Для простоты, наглядности и обозримости вычислений возьмем ограниченное количество величин n = 20, хотя для применения метода Пирсона необходимо, чтобы количество наблюдений было значительно больше (50 и более).
1. Получен ряд наблюдений случайной величины, который представлен табл.15.
Таблица 15
Ряд наблюдений
| № | ||||||||||
| xi | ||||||||||
| № | ||||||||||
| xi |
Преобразуем ряд наблюдений в вариационный ряд, т.е. установим результаты наблюдений в порядке возрастания (см. табл.16).
Таблица 16
Вариационный ряд
| № | ||||||||||
| xi | ||||||||||
| № | ||||||||||
| xi |
2. Вычислим статистические оценки распределения случайной величины: математическое ожидание mx, дисперсию Dx, СКО sx величины X
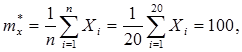
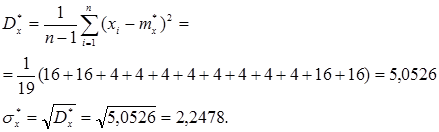
Произведем проверку критерия согласия с (нормальным) законом распределения по методу Пирсона.
*В общем случае число наблюдений должно быть значительно больше, причем на столько больше, чтобы в выделенные нами разряды (интервалы) попало не менее 8 - 10 наблюдений.
Построим статистический ряд, т. е. таблицу, в которой приведены длины разрядов Ji в порядке их соответствия оси абсцисс измеряемой величины X, количество ni значений величины хi, оказавшихся в том или ином разряде, а также статистические частоты Pi* и вероятности Pi попадания измеряемой величины X в интервал (хi: хi +1).
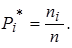
Вычисляем число разрядов k по формуле Стерджесса
k = 3,322 lg n + 1 = 3,322 lg20 + 1 = 3,322 ´ 1,3010 + 1 ≈ 5 = 5.
Находим, что число разрядов k = 5.
Разделение интервалов (хi: хi +1) производится по желанию оператора, но рекомендуется выбирать равномерно для облегчения вычислений.
Заполним табл.17 (первые три строчки).
Таблица 17
Статистический ряд
| Ji | 95 - 97 | 97 - 99 | 99 - 101 | 101 - 103 | 103 - 105 |
| ni | |||||
| Pi* | 0,10 | 0,20 | 0,40 | 0,20 | 0,10 |
| Pi | 0,0753 | 0,2395 | 0,3472 | 0,2395 | 0,0753 |
4. Построим гистограмму (рис. 23) и полигон (рис. 24), как графическое представление статистической плотности распределения.
Вид гистограммы и полигона позволяет выбрать в качестве теоретической модели нормальный закон распределений, который принимаем за рабочую гипотезу с целью идентификации.
5. Определяем значение границ интегрирования и вычисляем значения функции Лапласа Ф для этих значений по существующим таблицам (Приложение 1).
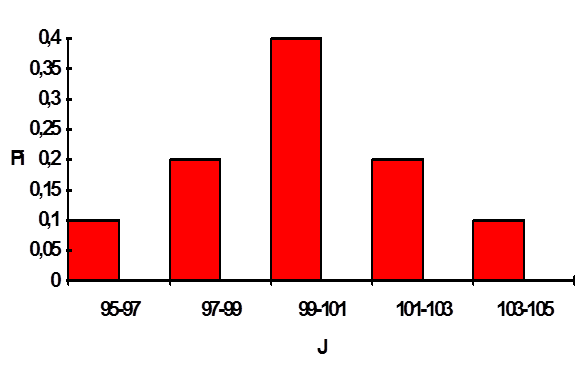
Рис.23. Гистограмма
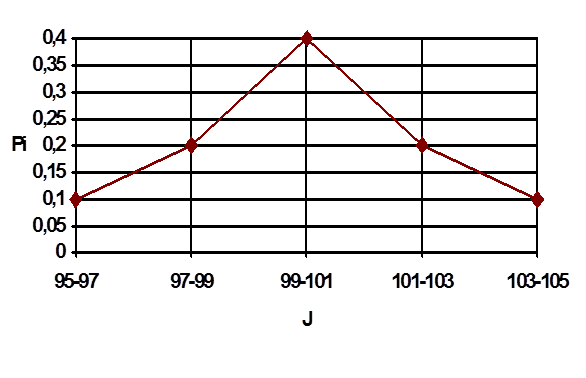
Рис. 24. Полигон
Вычисления теоретических вероятностей Pi производим по формуле:
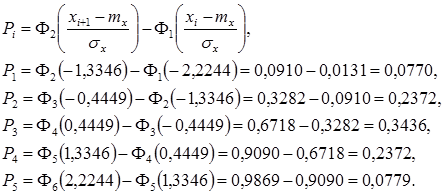
Результаты заносим в таблицу 17 (четвертая строка).
6. Вычисляем критерий согласия ХИ-квадрата (Пирсона).
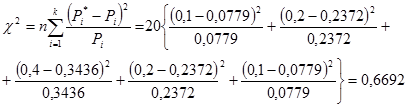
7. Находим число степеней свободы распределения ХИ-квадрат с учетом того, что достаточное число независимых условий s для нормального закона равно трем:
r = k - s = 5 - 3 = 2.
8. Из таблицы (Приложение 2) распределения ХИ-квадрат (для значений c 2 = 0,6692 и r = 2) находим вероятность согласия эмпирического и теоретического законов распределения P = 0,65, интерполируя между соседними величинами.
На основании полученной вероятности P = 0,65 можно сделать вывод, что гипотеза о соответствии эмпирического закона нормальному не противоречит экспериментальным данным.
9. Вычислим дисперсию и СКО результата измерений
,
.
10. Определим значения квантилей закона распределения t aпри доверительной вероятности P a= 0,95. Для нашего случая n - 1 = 20 - 1 = 19.
По таблице (Приложение 3) находим t a= 2,09.
11. Произведем интервальную оценку результата наблюдения x н. Вычислим доверительные границы и запишем результат наблюдения в виде
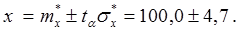
Это означает, что 95 % всех наблюдаемых значений распределяются в пределах от 95,3 до 104,7.
12. Произведем интервальную оценку результата измерений x из, предварительно вычислив доверительные границы. Результат измерения представим в виде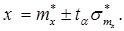 
, т.е.
.
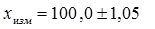Таким образом с достоверностью 95 % можно утверждать, что математическое ожидание среднего арифметического результата измерений находится в пределах от 99 до 101 В.
Вопросы к разделу
1. Перечислите этапы обработки результатов прямых многократных измерений.
2. Что такое вариационный ряд и интервалы группирования?
3. Как определяется число интервалов группирования?
4. Что такое гистограмма, полигон и кумулятивная кривая?
5. Для чего необходимо идентифицировать форму закона распределения результатов измерений?
13. ПРИМЕРЫ ВЫЧИСЛЕНИЙ МЕТРОЛОГИЧЕСКИХ
ХАРАКТЕРИСТИК РАСХОДОМЕРОВ
13.1. РАСЧЕТ ПО УЧЁТУ ПРИРОДНОГО ГАЗА СУЖАЮЩИМИ УСТРОЙСТВАМИ
Расчет выполнен в соответствии с ГОСТ 8.563.1 -97, ГОСТ 8.563.2 – 97.*
*(В настоящее время вступил в действие ГОСТ 8.586.1-5 – 2005 Измерение расхода и количества жидкостей и газов с помощью стандартных сужающих устройств. Части 1-5).
Данные для расчёта по учёту природного газа
Характеристика измеряемой среды:
Измеряемая среда - природный ГАЗ сухой
Молярная концентрация компонентов:
- метан(СН4), хм = 99,00 %
- азот(N2), ха = 0,79 %
- диоксид углерода(СО2), ху = 0,21 %
Сужающее устройство: Диафрагма с угловым способом отбора
1. Барометрическое давление: рб = 748 мм рт. ст.;
2. Избыточное давление: ри = 0,4 МПа;
3. Температура: t = 10 град. С;
4. Плотность в стандартных условиях: ρс = 0,67992 кг/м 3;
5. Перепад давления при верхнем
значении измеряемого расхода: Δр = 100 кПа;
6. Количество дифманометров: 1
7. Диаметр сужающего устройства
в стандартных условиях: d2 0 = 61,354 мм;
8. Начальное значение радиуса закругления
входной кромки диафрагмы: rн = 0,05 мм;
9. Диаметр измерительного трубопровода
в стандартных условиях: D20 = 100 мм;
10.Абсолютная эквивалентная шероховатость
стенок трубопровода: Rш = 0,1 мм;
11. Верхний предел измеряемого расхода: qв = 8000 м 3 /ч;
12. Нижний предел измеряемого расхода: qн = 3000 м 3 /ч;
13. Погрешность измерения расхода в
заданном диапазоне не превышает: 5 %
14. Давление при стандартных условиях
по ГОСТ 30319.0 - 96: рс = 0,101325 МПа;
15.Температура при стандартных условиях
по ГОСТ 30319.0 - 96: Тс = 293,15 К.
ЧИСЛЕННЫЙ РАСЧЕТ
1. Абсолютное давление, p, МПа:
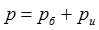
рб= 748 мм.рт.ст = 748×13.595×10-4 = 1,0169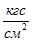 
= 0,09972 МПа
ри = 0,4 МПа
р = 0,09972 + 0,4 = 0,49972 МПа
2. Термодинамическая температура природного газа, Т, К:
Т =273,15 + t °C
Т = 273,15 + 10°С = 283,15 К
3. Динамическая вязкость природного газа, m, Па·с:
определяется по ГОСТ 30319.1 и ГОСТ 30319.3
m = mТ·сm,
где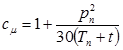 
- поправочный множитель;
mТ - составляющая динамической вязкости природного газа, мкПа·с
.
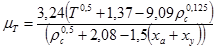Приведенные давление рп и температура Тп вычисляются по формулам
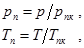
где псевдокритические давление рпк и температура Тпк рассчитываются, соответственно, по формулам (48) и (49) ГОСТ 30319.2, а именно:
pпк = 2,9585(1,608 - 0,05994 ρс + xу - 0,392 xа),
Тпк = 88,25(0,9915 + 1,759 ρс - ху - 1,681 xа).
Произведем вычисления
рпк = 2,9585(1,608 - 0,05994×0,67992 + 0,21 - 0,392×0,79) = 4,34179 МПа,
Tпк = 88,25(0,9915 +1,759×0,67992- 0,21 - 1,681×0,79) = 57,3173 К,
рп = 0,49972 / 4,34179 = 0,11509 МПа
Тп = 283,15 / 57,3173 = 4,940 К
сm = 1+(0,0132457/118,2) = 1 + 0,000112 = 1,000112
mТ = 21,99433 мкПа·с = 0,00002199433 Па·с
m = 0,00002199433×1,000112 = 0,0000219968 Па·с
4. Показатель изоэнтропии (адиабаты) природного газа k (определяется по ГОСТ 30319.1 и ГОСТ 30319.3):
k = 1,556(1+0,074 xа) - 3,9×10-4 Т (1- 0,68 xа) - 0,208 ρс +
+ (ρ / Т)1,43[384(1 - xа) (ρ / Т)0,8 + 26,4 xа ],
k = 1,556(1+0,074×0,79) - 3,9×10-4×283,15(1- 0,68×0,79) - 0,208×0,67992 +
+ (0,49972/283,15)1,43 × [384(1- 0,79)(0,49972/283,15)0,8+ 26,4×0,79] =
= 1,456902584
5. Определение диаметров измерительного трубопровода (ИТ) и сужающего устройства (СУ) при стандартных и рабочих температурах.
5.1 Диаметр измерительного трубопровода, мм:
D = D20 Кt,
где Кt - поправочный коэффициент на изменении диаметра ИТ;
Кt = 1 + γ (t - 20),
где γ - температурный коэффициент линейного расширения материала (Сталь 20)
γ = 10-6 [ ае + 10-3 t bе - 10-6 t 2 се ]
(ае, bе, се - постоянные коэффициенты в соответствующих им диапазонах температур, приведенные в таблице В.1 ГОСТ 8.563.1 – 97).
γ = 10-6 [11,1 + 10-3×10×7,7- 10-6×102×3,4] = 11,17666·10-6
t =10°С
Кt = 1 + 11,17666×10-6(10 -20)= 0,999888
D20 = 100 мм
D = 100×0,999888 = 99,9888 мм
5.2 Диаметр отверстия сужающего устройства d, мм:
d = d20 К0,
где К0- поправочный коэффициент на изменение диаметра отверстия СУ
К0 = 1+ γ (t - 20),
где γ - температурный коэффициент линейного расширения материала (Сталь 12Х18Н9Т);
γ = 10-6 [15,6 + 10-3·10·8,3 - 10-6·102·6,5] = 10-6 [15,6+0,083+0,00065] = 15,6823·10-6
К0 = 1 + 15,6823·10-6 (10-20) = 0,999843
d20 = 61,354 мм
d = 61,354·0,999843 = 61,344 мм
6. Относительный диаметр отверстия сужающего устройства, β:
7. Коэффициент скорости входа, E:
,
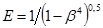8. Коэффициент истечения, рассчитанный при числе Рейнольдса, стремящемся к бесконечности (для углового отбора давления):
С~ = 0,5959 +0,0312· β 2,1 - 0,1840· β 8,
С~ = 0,5959 +0,0312·0,6135362,1 - 0,1840·0,6135368 = 0,60339
9. Поправочный коэффициент на не остроту входной кромки диафрагмы, К П:
,
где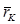 
- средний за межповерочный интервал радиус закругления входной кромки диафрагмы, мм
,
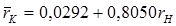rH = 0,05 мм
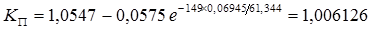
К П = 1,006126
10. Коэффициент расширения природного газа, ε:
,
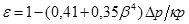ε = 1 - (0,41 + 0,35·0,6135364)×100/(1,46562758×449,72) = 0,93687378
11. По ГОСТ 8.563.1- 97 проверяем условие:
.
Если условие выполняется, то К ш = 1,
не выполняется, то К ш = 1 + β 4 r 0АRe
Проверяем условие:
получаем 10,0011 > 0,9753264 т.е. условие не выполняется, поэтому вычислим коэффициент К ш:
рассчитаем r0 для диафрагм (по ГОСТ 8.563.1-97) по формуле
,
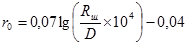АRе = 1, при Rе > 106 (по ГОСТ 8.563.1-97) Кш = 1+ 0,6135364×0,03×1 = 1,004250.
12. Плотность при рабочих условиях ρ, кгм -3 :
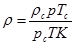
где К - коэффициент сжимаемости, равен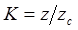 
.
Значение К определяется согласно ГОСТ 30319.2 - 96 «Газ природный. Методы расчета физических свойств. Определение коэффициента сжимаемости» (К = 0,99139586).
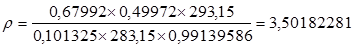кгм -3
13. Число Рейнольдса, Re:
,
где Кe3 - масштабный коэффициент, значения которого приведены в таблице А.6 ГОСТ 8.563.2-97 (Ке3=1,2732×103).
14. Потеря давления Δω, кПа:
,
Δω = (1 - 0,6135361,9)×100 = 60,48 кПа
15. Поправочный коэффициент на число Рейнольдса, К Re:
,
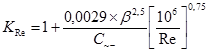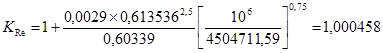
16. Коэффициент расхода, а:
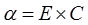
α = 1,079393×0,603666 = 0,651876
17. Коэффициент истечения, С:
С = С ~ K Re
С = 0,60339×1,000458 = 0,603666
18. Объёмный расход в стандартных условиях, qс , м3/ч:
,
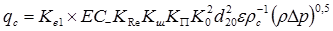где К с1 - масштабный коэффициент, значения которого приведены в таблице А.4 ГОСТ 8.563.2-97 (К е1 = 1,2645×10-1);
qc = 0,12645×1,079393×0,60339×1,000458×1,006126×1,0042499×0,9998432×
×61,3542×0,93687378× (0,67992)-1×(3,502037648×100)0,5 = 8078,254642 м3/ч
19. Массовый расход, qт, кг/ч:
qт = qс · ρс = q0 · ρ
qт = 8127,74203×0,67992 = 5526,21436 кг/ч = 1,525713 кг/с
Не трудно видеть, что расчет достаточно громоздок и утомителен, тем не менее, при отсутствии утвержденной аттестованной программы такой расчет необходимо произвести. В производственных условиях расчет производится на ЭВМ по специальной утвержденной программе. Как правило расчеты ручным способом и машинным способом на ЭВМ несколько отличаются из-за погрешностей вычислений. В этом случае за результат необходимо принять расчет, выполненный на ЭВМ по специальной стандартизованной программе. Это необходимо сделать для обеспечения единства измерений, кроме того, действует старинное правило метрологии: - две величины в пределах погрешности равны.
13.2. РАСЧЕТ СУЖАЮЩЕГО УСТРОЙСТВА ПО ПРОГРАММЕ
Программный комплекс "Расходомер-СТ", в.4.47 от 26.12.00, с/н:004-470533 (Pазработчик: ВНИИ расходометрии, Казань)
Владелец данной копии программы: ФГУ «Татарстанский ЦСМ»
Расчет N 1 от 2.12.2005,
выполнен в соответствии с ГОСТ 8.563.1-97, ГОСТ 8.563.2-97.
ЗАОр НП НЧ КБК (Т-315)
Характеристика измеряемой среды
Измеряемая среда - природный ГАЗ сухой
Молярная концентр. компонентов (погрешность сист., случ.):
- Метан 99,00 %
- азот............(0.050, 0.000)........ 0.79 %
- СО2.............(0.050, 0.000)........ 0.21 %
Барометрическое давление................. 750.076 мм рт.ст
Избыточное давление....................... 0.4 МПа
* Абсолютное давление....................... 0.5 МПа
Температура............................... 5.0 град.C
Плотность в стандартных условиях.......... 0.6792 кг/м3
погрешность определения систематическая..0.05 %
погрешность определения случайная........0.0 %
* Плотность в рабочих условиях.............. 3.56565 кг/м3
* Коэффициент сжимаемости................... 0.99065569
Метод расчета коэффициента сжимаемости.... NX19 мод.
* Показатель адиабаты....................... 1.3081
* Динамическая вязкость..................... 0.00001054 Па∙с
Перепад давления.......................... 100 кПа
Количество дифманометров.................. 1
Верхний предел первого дифманометра.. 100.0 кПа
Характеристика сужающего устройства
Сужающее устройство:
Диафрагма с угловым способом отбора давления
ДИАМЕТР сужающего устройства
в стандартных условиях.................... 61.355 мм
* Диаметр сужающего устройства
в рабочих условиях........................ 61.341 мм
Материал сужающего устройства........... Сталь 12Х18Н9Т
* Поправочный коэффициент на расширение
материала сужающего устройства............ 0.99977
Радиус закругления входной кромки......... 0.05 мм
Период поверки, в годах................... 1
* Поправочный коэффициент на неостроту
входной кромки диафрагмы.................. 1.00639
Способ определения радиуса входной кромки диафрагмы визуальным или табличным методом
Характеристика трубопровода
Диаметр трубопровода в стандартн. условиях 100.0 мм
* Диаметр трубопровода в рабочих условиях... 99.983 мм
Материал трубопровода..................... Сталь 20
* Поправочный коэффициент на расширение
материала трубопровода.................... 0.99983
Абсолютная эквивалентная шероховатость
стенок трубопровода....................... 0.15 мм
* Поправочный коэффициент на шероховатость
трубопровода.............................. 1.006
Способ определения шероховатости трубопровода визуальным или табличным методом
Характеристика измерительного участка
Местные сопротивления, расположенные на расстоянии 100D до СУ:
Первое (против потока) местное сопротивление
Группа колен в одной плоскости
Второе (против потока) местное сопротивление
Конфузор
Местное сопротивление после сужающего устройства
Есть
Расстояние между первым местным сопротивлением и сужающим устройством............................... 6240 мм
диаметр трубопровода между 1-м и 2-м местным
сопротивлением... 100 мм
Расстояние между 1-м и 2-м местными сопротивлениями 100.0 мм
Расстояние между сужающим устройством и местным сопротивлением после него................................ 1850 мм
· Суммарная погрешность, вводимая в связи с сокращением длин прямых участков трубопроводов............. 0.0 %
Место установки гильзы термометра
До сужающего устройства
Диаметр гильзы термометра................. 12 мм
Длина прямого участка от сужающего устройства до места установки гильзы термометра.............. 4000 мм
* Погрешность вводимая в связи с сокращением прямого участка трубопровода между сужающим устройством и гильзой термометра........................ 0.0 %
Комплексные параметры расходомера
* Относительный диаметр сужающего устройства 0.6135
* Число Рейнольдса................... 1850791.3
* Коэффициент расхода сужающего устройства.. 0.6519
* Коэффициент расширения.................... 0.9297
* Коэффициент истечения..................... 0.6039
* Потери давления........................... 60.20418 кПа
Обьемный расход:
* - в стандартных условиях.................. 8116.2338 м3/ч
* Массовый расход........................... 1.5312628 кг/с
Расчет погрешностей.
Верхний предел измерений барометра................ 800.00 мм рт.ст
Нижний предел измерений барометра................ 600.00 мм рт.ст
Погрешность измерения барометрического давления:
систематическая.... 0.000 %
случайная........ 0.000 %
Избыточное давление:
Верхний предел измерения.................... 1.00000 МПа
