В ряде случаев для защиты решения задачи от переполнения памяти и достижения точности вычислений на ЭВМ исходные данные выгоднее пронормировать [12].
Тогда новые переменные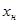 
и 
через исходные 
и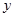 
, нормирующие множители 
и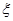 
выражаются преобразованием
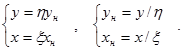
В общем случае нормирующие множители и 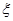выбирают произвольно, руководствуясь правилом, чтобы новые переменные были соразмерны с единицей.
В большинстве случаев удобнее в качестве нормирующих множителей брать средние значения переменных
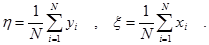
Рассмотрим, как влияет нормирование переменных на результат вычислений. Обозначим все новые значения коэффициентов через те же символы, но с волнистой чертой сверху.
Используя метод математической индукции можно доказать, что
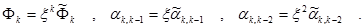
Подставляя новые значения в формулу (7.7), можно получить закон преобразования коэффициентов при ортогональных полиномах в виде
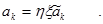
Далее, применяя еще раз метод математической индукции, также можно получить правило преобразования коэффициентов ортогональных полиномов и аппроксимирующего полинома:
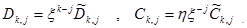
Таким образом, в случае обработки нормированных опытных данных имеем следующие формулы восстановления аппроксимирующих значений:
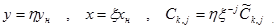
Приведенный метод нормирования исходных данных реализован в подпрограмме OR [12].
