Рассмотрим вопрос об аппроксимации функции многих переменных, значения которой заданы в табличной форме, ортогональными полиномами методом наименьших квадратов [11].
Предположим, что в результате наблюдений получена таблица значений функции от n аргументов в N точках с некоторой погрешностью
 (7.15)
(7.15)
где  и пусть число точек N достаточно велико.
и пусть число точек N достаточно велико.
Найдем полином k -й степени  от n переменных, минимизирующее выражение
от n переменных, минимизирующее выражение
 (7.16)
(7.16)
где 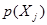 - весовая функция.
- весовая функция.
Употребляя обозначения Гаусса (вместо символа  для обозначения суммирования по числу N точек следует писать квадратные скобки, а индексы опускать), выражение (7.16)запишем следующим образом:
для обозначения суммирования по числу N точек следует писать квадратные скобки, а индексы опускать), выражение (7.16)запишем следующим образом:
 (7.17)
(7.17)
Функцию  ищем в виде
ищем в виде
 (7.18)
(7.18)
где  - ортогональный полином i -й степени.
- ортогональный полином i -й степени.
Запишем условие ортогональности
 (7.19)
(7.19)
Из условий (7.19)следует, что
 при
при 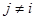 (7.20)
(7.20)
Подставляя (7.18) в (7.20), учитывая условие ортогональности  , найдем коэффициент а.
, найдем коэффициент а.
 (7.21)
(7.21)
Обратимся к построению ортогональных полиномов. Положим 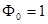 , а
, а  распишем для общего случая
распишем для общего случая
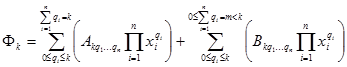 (7.22)
(7.22)
Пронумеруем коэффициенты 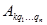 и
и  . Для этого представим индексы
. Для этого представим индексы  как числа в (k+1) -ой системе счисления, расположим их в возрастающем порядке и пересчитаем. Всего коэффициентов
как числа в (k+1) -ой системе счисления, расположим их в возрастающем порядке и пересчитаем. Всего коэффициентов  будет
будет 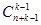 (в дальнейшем будем их обозначать через
(в дальнейшем будем их обозначать через  где
где  ), а коэффициентов
), а коэффициентов 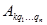 будет
будет  (в дальнейшем будем их обозначать
(в дальнейшем будем их обозначать  , где
, где  ).
).
Также поступим с произведениями
 (7.23)
(7.23)
где  индекс соответствующих коэффициентов
индекс соответствующих коэффициентов  .
.
Перепишем (7.22) в новых обозначениях:
 (7.24)
(7.24)
Из условия ортогональности имеем 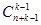 уравнений для определения
уравнений для определения  неизвестных коэффициентов
неизвестных коэффициентов  и
и  .
.
 , (7.25)
, (7.25)
где  , или в развернутом виде
, или в развернутом виде
 .
.
В дальнейшем под символом  будем понимать матрицу, составленную из элементов
будем понимать матрицу, составленную из элементов  , в которой m- й столбец заменен элементами
, в которой m- й столбец заменен элементами 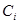 .
.
При введенных обозначениях из системы (7.25) получаем коэффициенты  в следующем виде:
в следующем виде:
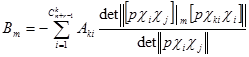 (7.26)
(7.26)
ортогональный многочлен  - в виде
- в виде
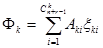 (7.27)
(7.27)
где
 (7.28)
(7.28)
Найдем коэффициенты  , для чего подставим (7.27) в (7.25)
, для чего подставим (7.27) в (7.25)
 (7.29)
(7.29)
где
 (7.30)
(7.30)
Дифференцируя F по  и приравнивая производные нулю, получим нормальную систему линейных уравнений
и приравнивая производные нулю, получим нормальную систему линейных уравнений
 (7.31)
(7.31)
где  откуда
откуда
 (7.32)
(7.32)
Таким образом, ортогональные полиномы и аппроксимирующий многочлен определяются из формул (7.18), (7.27), (7.28), (7.30), (7.32).






