Косвенными измерениями называются измерения, при которых искомое значение величины находят на основании известной зависимости между этой величиной и величинами, полученными прямыми измерениями.
Пусть требуется оценить значение величины Y, связанной с измеренными величинами X1,..., Xk зависимостью: 
.
Необходимо найти оценку 
неизвестной величины (истинного значения) Y, если при обработке результатов прямых измерений получены оценки в виде средних арифметических значений 
величин 
.
Поскольку измеренные и истинные значения связаны между собой с помощью погрешностей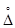 
измерений, то имеем:
,
где 
Разложим полученные выражения в “ k ” - мерный ряд Тейлора, ограничиваясь тремя членами (второго порядка малости)
,
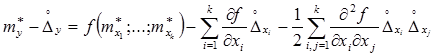отсюда:
;
.
В большинстве случаев, когда не требуется высокая точность, ограничиваются членами первого порядка малости
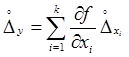
Примечание: Складываются абсолютные значения.
Вычислим дисперсию 
оценки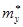 
величины Y.
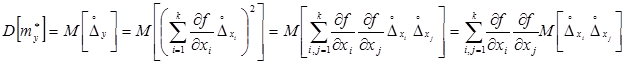
Рассмотрим величину
В случае, когда i = j значение r = 1 и 
Таким образом, дисперсия оценки математического ожидания результатов косвенных измерений будет равна:
или
Для независимых величин x1,...,xk, когда 
статистическая дисперсия будет равна:
Для СКО при отсутствии корреляции имеем
,
если случайные величины коррелированны, то
Погрешности при косвенных измерениях вычисляют по формулам: при отсутствии корреляции между случайными величинами
;
при коррелированных значениях случайных величин
.
Данные формулы широко применяются при расчете погрешностей измерений.
Величины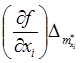 
- называются частными погрешностями.
Например для функции от двух переменных z=f (x,y) при отсутствии корреляции rxy = 0, погрешность результата измерений вычисляется по формуле:
,
где 
– погрешности переменных x и y;
- частные производные функции по переменным 
, соответственно;
- частные погрешности .
