Проверка гипотезы о нормальном распределении генеральной совокупности. Критерий Пирсона

Для проверки гипотезы о нормальном распределении случайных величин в пакете STATISTICA используется модуль Descriptive Statistics (Описательные статистики). При этом используется критерий согласия Колмогорова-Смирнова, предполагающий, что параметры нормального распределения известны. Проверим гипотезу о нормальном законе распределения размеров головок заклепок, сделанных на одном станке, по выборке объема n = 200; измерения приведены в табл. 1.1. Оценками для а (среднего) и s (стандартного отклонения) являются

 

и .

 

Таблица 1.1

Диаметры 200 головок заклепок, мм
13.39	13.33	13.56	13.38	13.43	13.37	13.53	13.40	13.25	13.39
13.28	13.34	13.50	13.38	13.38	13.45	13.47	13.62	13.45	13.39
13.53	13.58	13.32	13.27	13.42	13.40	13.57	13.46	13.33	13.40
13.57	13.36	13.43	13.38	13.26	13.52	13.35	13.29	13.48	13.43
13.40	13.39	13.50	13.52	13.39	13.39	13.46	13.29	13.55	13.31
13.29	13.33	13.38	13.61	13.55	13.40	13.20	13.31	13.46	13.13
13.43	13.51	13.50	13.38	13.44	13.62	13.42	13.54	13.31	13.58
13.41	13.49	13.42	13.45	13.34	13.47	13.48	13.59	13.20	1 4.56
13.55	13.44	13.50	13.40	13.48	13.29	13.31	13.42	13.32	13.48
13.43	13.26	13.58	13.38	13.48	13.45	13.29	13.32	13.24	13.38
13.34	13.14	13.31	13.51	13.59	13.32	13.52	13.57	13.62	13.29
13.23	13.37	13.64	13.30	13.40	13.58	1.24	13.32	13.52	13.50
13.43	13.58	13.63	13.48	13.34	13.37	13.18	13.50	13.45	13.60
13.38	13.33	13.57	13.28	13.32	13.40	13.40	13.33	13.20	13.44
13.34	13.54	13.40	13.47	13.28	13.41	13.39	13.48	13.42	13.46
13.28	13.46	13.37	13.53	13.43	13.30	13.45	13.40	13.45	13.40
13.33	13.39	13.56	13.46	13.26	13.35	13.42	13.36	13.44	13.41
13.43	13.51	13.51	13.24	13.34	13.28	13.37	13.54	13.43	13.35
13.52	13.23	13.48	13.48	13.54	13.41	13.51	13.44	13.36	13.36
13.53	13.44	13.69	13.66	13.32	13.26	13.51	13.38	13.46	13.34

 

Результаты измерения диаметров заклепок занесем в таблицу с одним столбцом (d) и 200 строками.

Для проверки гипотезы о нормальном распределении исходных данных будем использовать процедуру Distribution Fitting (подбор распределения), которая находится в меню Statistics.

Зададим диапазон исходных данных, нажав на кнопку Variable и выбрав там единственно возможную: d (рис. 1.11). Далее нажмем кнопку ОК.

 

Рис. 1.11.

 

Выберем во вкладке Continuous Distributions: требуемый тип распределения
Normal (нормальное). Это можно также осуществить с помощью вкладки Quick.

Во вкладке Options откажемся от теста Колмогорова-Смирнова. Для этого установим соответствующий переключатель в положение None. При этом выключатель теста χ² (Chi-Square) должен быть активизирован. Для построения графика отметим опцию Frequency d istribution (частоты распределения)

Во вкладке Parameters установим количество интегралов разбиения равное 19. В этом же окне наблюдаем значения нижней и верхней границы значений исходных данных, наблюдаемые значение математического ожидания и дисперсии. Нажав кнопку Summary во вкладке Quick, получаем таблицу частот. Первый столбец данных содержит левые границы интервалов группирования данных, второй – наблюдаемые частоты попадания данных в интервал, третий – накопленные частоты.

В таблице на рис. 1.12 приведено значение статистики χ² = 11.99951, количество степеней свободы df = 3, которое получилось при объединении интервалов и приведено значение вероятности 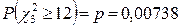. последнее означает, что если гипотеза верна, вероятность получить 12.00 или больше равна 0.00738 – слишком мала, чтобы поверить в нормальность распределения исходных данных. Следовательно, гипотезу о нормальности отклоняем.

 

Рис.1.12. Результаты расчетов

Построим гистограмму наблюдений и сравним распределение наблюдаемых и ожидаемых частоты с помощью графиков. Для этого во вкладке Quick нажмем кнопку Plot of observed and expected distribution. Очевидно, что гистограмма, построенная по исходным данным, значительно отличается от кривой плотности нормального распределения, которая на полученном графике отмечена красной линией (рис.1.13).

 

Рис. 1.13 Гистограмма частот и график плотности нормального распределения

 

Если посмотреть гистограмму наблюдений, видно, что в выборке имеется одно аномальное значение 14.56 (№ 188), которое могло появиться в результате какой-либо ошибки (при записи наблюдений, при перепечатке или попалась деталь с другого станка и т.д.). Удалим его и снова проверим гипотезу. Удаление одного наблюдения, если оно типично, не может изменить характеристики совокупности из 200 элементов; если же изменение происходит, следовательно, это наблюдение типичным не является и должно быть удалено.

Чтобы не искажать исходные данные, продублируем их в новый столбец, который назовем, например, dc, и удалим аномальное наблюдение.

 

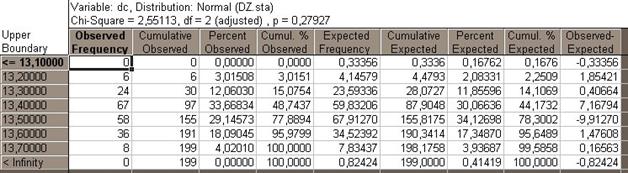
Рис. 1.14 Расчеты по скорректированным данным

 

Повторим проверку гипотезы для полученной выборки и убедимся в том, что наблюдения не противоречат гипотезе о нормальности, так как в данном случае значение вероятности 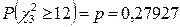. Этот же вывод подтверждается с помощью графиков. В данном случае гистограмма, построенная по исходным данным, лучше подходит к кривой плотности нормального распределения.