Зубчатые передачи находят широкое применение в различных видах машин и механизмов, исполняя роль передаточного механизма. Они определяют качество, надежность, работоспособность и долговечность машин, станков, приборов и других изделий. Расчет геометрических параметров зубчатых передач необходим с конструкторской точки зрения, так как определяет основные размеры и габариты передачи, а также с технологических позиций, так как влияет на выбор оборудования и методов обработки.
Наиболее широко применяются эвольвентные цилиндрические зубчатые передачи внешнего и внутреннего зацепления с исходным контуром, профилирующим режущий инструмент по ГОСТ 13755. Исходный контур выполняется в виде прямозубой рейки с углом α = 20°. Прямозубые колеса имеют направление зуба вдоль оси колеса. У косозубых колес зуб направлен под утлом βк оси колеса.
Основным геометрическим параметром, определяющим все элементы передачи, является модуль - т, который выбирается в зависимости от передаваемой нагрузки из нормального ряда модулей по ГОСТ 9563.
Модуль – это число, показывающее, сколько миллиметров диаметра делительной окружности приходится на один зуб зубчатого колеса.
Зубчатые колеса с модулем от 0,05 мм до 1 мм принято называть мелкомодульными; от 1 до 10 мм – среднемодульными и свыше 10 мм – крупномодульными.
Основное применение находит первый ряд модулей: 0,5; 0,6; 0,8; 1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16. Второй ряд применяется ограниченно: 0,55; 0,7; 0,9; 1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5; 7; 9; 11; 14; 18.
Мелкомодульные передачи (m < 1) используются при малых нагрузках (в приборостроении, при ручном приводе). Чем больше передаваемая нагрузка, тем больше должен быть модуль и ширина зубчатого венца – В. Рекомендуется принимать В = (3... 15) т.
Число зубьев колес принято обозначать буквой Z, а в передаче для ведущего (шестерни) и ведомого колес –Z1 и Z 2 соответственно.
В зубчатой передаче число оборотов зависит от числа зубьев колеса.
Передаточное число i =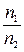 
= 
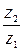, где n1 и n2 – число оборотов в минуту ведущего и ведомого колеса.
Межосевое расстояние (делительное) в передаче а = m(Z1 + Z2)/2.
К основным параметрам зубчатого колеса относятся:
- диаметр делительной окружности –d = mZ;
- диаметр окружности выступов –da = d + 2т =m(Z + 2);
- диаметр окружности впадин –df= d – 2,5т = m(Z – 2,5);
- окружной шаг (шаг по делительной окружности) pt = 360/ z = π m;
- диаметр основной окружности –db = d cosα = m z cosα;
- шаг зацепления или основной шаг (шаг по основной окружности):
рα = рb = рt cosα = πm cos α;
- высота головки зуба ha = m;
- высота ножки hf = 1,25 т;
- толщина зуба по делительной окружности S =рt/2 = π т/2 на высоте головки зуба hα;
- толщина зуба по постоянной хорде Sc = 1,387 m, измеренная на высоте hc = 0,7476 m от вершины зуба. Этот показатель не зависит от числа зубьев колеса, а зависит только от модуля;
- размер по роликам –М (для определения значения окружной толщины зуба или величины смещения исходного контура для мелкомодульных колес);
- длина общей нормали W или средняя длина общей нормали Wm.
Длина общей нормали – это расстояние между двумя параллельными плоскостями, касательными к двум разноименным, активным боковым поверхностям зубьев колеса. Номинальное значение длины общей нормали определяется по формуле:
W = pt (Zw – 1)+ S,
где Z w = 0,111 z + 0,5 или Z w = z /9 + 1 – число охватываемых при измерении зубьев, которое необходимо округлять до ближайшего целого числа (таблица 7.1). Для колес с углом зацепления α = 20° формула принимает вид:
W = m [1,476 (2 Z w – 1) + 0,014 Z ].
Длина общей нормали прямо пропорциональна модулю, поэтому в таблицах справочников указывается значение длины общей нормали для т = 1 (см. таблицу 7.1). При изменении модуля табличное значение необходимо умножить на величину модуля.
Средняя длина общей нормали определяется по результатам измерения всех длин у колеса от зуба к зубу, как среднее арифметическое значение:
Wm =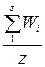 
.
Ввиду погрешностей обработки, у одного зубчатого колеса длина общей нормали изменяется от зуба к зубу.
Для размещения смазки и исключения заклинивания требуется увеличивать или уменьшать толщину зуба. Теоретическое зацепление считается двухпрофильным, когда контакт идет по обеим сторонам зуба.
Реальная передача имеет однопрофильное зацепление, т.е. по рабочим профилям – контакт, а по нерабочим – зазор.
Таблица 7.1 – Геометрические параметры зубчатого колеса при m = 1, α = 20 °С
| Число зубьев Z колеса | Количество охватываемых зубьев Z w | Длина общей нормали W, мм | Диаметр основной окружности db, мм | Число зубьев Z колеса | Количество охватываемых зубьев Zw | Длина общей нормали W, мм | Диаметр основной окружности db, мм | ||
| 4,596 | 11,276 | 47,924 | |||||||
| 4,938 | 14,095 | 16,965 | 48,864 | ||||||
| 4,652 | 15,035 | 16,978 | 49,804 | ||||||
| 4,666 | 15,975 | 16,992 | 50,743 | ||||||
| 4,680 | 16,914 | 19,959 | 51,683 | ||||||
| 7,660 | 18,794 | 19,973 | 52,623 | ||||||
| 7,688 | 20,673 | 19,987 | 53,562 | ||||||
| 7,702 | 21,613 | 20,001 | 54,502 | ||||||
| 7,716 | 22,557 | 20,015 | 55,442 | ||||||
| 7,730 | 23,492 | 20,029 | 56,382 | ||||||
| 7,744 | 24,432 | 20,057 | 58,261 | ||||||
| 7,758 | 23,051 | 61,08 | |||||||
| 10,725 | 26,311 | 23,065 | 62,02 | ||||||
| 10,739 | 27,251 | 23,093 | 63,899 | ||||||
| 10,753 | 28,191 | 23,121 | 66,778 | ||||||
| 10,767 | 29,13 | 23,149 | 67,578 | ||||||
| 10,781 | 30,07 | 26,051 | 70,477 | ||||||
| 10,795 | 31,001 | 26,157 | 71,416 | ||||||
| 10,809 | 31,95 | 26,185 | 73,296 | ||||||
| 10,872 | 32,889 | 26,199 | 74,236 | ||||||
| 10,836 | 33,829 | 26,213 | 75,175 | ||||||
| 13,803 | 34,769 | 29,194 | 77,055 | ||||||
| 13,817 | 35,708 | 29,236 | 79,874 | ||||||
| 13,831 | 36,648 | 29,306 | 84,572 | ||||||
| 13,845 | 37,588 | 32,286 | 86,452 | ||||||
| 13,859 | 38,527 | 32,314 | 88,331 | ||||||
| 13,873 | 39,467 | 32,328 | 89,271 | ||||||
| 13,887 | 40,407 | 32,369 | 92,09 | ||||||
| 13,900 | 41,346 | 32,398 | 93,97 | ||||||
| 13,914 | 42,286 | 35,350 | 93,97 | ||||||
| 16,881 | 43,226 | 35,420 | 98,668 | ||||||
| 16,895 | 44,166 | 38,414 | 101,468 | ||||||
| 16,909 | 45,105 | 38,442 | 103,336 | ||||||
| 16,923 | 46,045 | 38,470 | 105,246 | ||||||
| 16,937 | 46,985 | 38,512 | 108,066 | ||||||
Величина бокового зазора зависит от условий эксплуатации: температуры, смазки, нагрузки, условий загрязнения и других требований (см. п. 7.3).
У зубчатого колеса различают окружной шаг по делительной окружности:
p t = 360/ Z = π m,
и шаг зацепления или основной шаг (шаг по основной окружности):
Pb = Pt cos α = π т cos α.
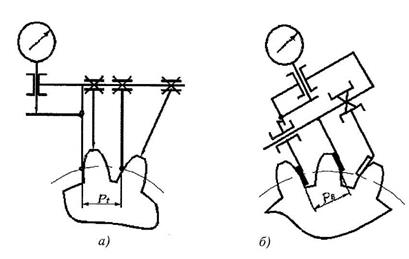
Рисунок 7.1 – Схема измерения шаговых параметров зубчатого колеса:
а – окружного шага; б – шага зацепления
Контроль окружного шага может быть выполнен накладным шагомером или универсальным зубоизмерительным прибором. Базирующие наконечники опираются на наружный (или внутренний) диаметр (рисунок 7.1, а). Широко используется метод измерения от «первого шага», принятого за номинальное значение с определением отклонений от него. Измерив по всей окружности Z раз, можно построить график и определить накопленную погрешность окружного шага.
Шаг зацепления (основной шаг) контролируется в плоскости, касательной к основному цилиндру (рисунок 7.1, б). Настройка прибора производиться на ноль по блоку кольцевых мер длины, равному номинальному значению шага зацепления. Метод измерения относительный, так как прибор показывает погрешность шага зацепления:
∆pb = pbr – pb ном
