Одним из путей повышения надежности системы является введение в нее резервных (дублирующих) элементов. Резервные элементы включаются в систему как бы «параллельно» тем, надежность которых недостаточна.
4.5.4.1. Параллельное соединение резервного оборудования системы Рассмотрим самый простой пример резервированной системы — параллельное соединение резервного оборудования системы. В этой схеме все n одинаковых образцов оборудования работают одновременно, и каждый образец оборудования имеет одинаковую интенсивность отказов. Такая картина наблюдается, например, если все образцы оборудования держатся под рабочим напряжением (так называемый «горячий резерв»), а для исправной работы системы должен быть исправен хотя бы один из n образцов оборудования.
В этом варианте резервирования применимо правило определения надежности параллельно соединенных независимых элементов. В нашем случае, когда надежности всех элементов одинаковы, надежность блока определяется по формуле (4.5.10)

Если система состоит из n образцов резервного оборудования с различными интенсивностями отказов, то:

Выражение (4.5.22) представляется как биноминальное распределение. Поэтому ясно, что когда для работы системы требуется по меньшей мере k исправных из n образцов оборудования, то:

При постоянной интенсивности отказов l элементов это выражение принимает вид:

где: p = exp(−λ t).
4.5.4.2. Включение резервного оборудования системы замещением В данной схеме включения n одинаковых образцов оборудования только один находится все время в работе (рис. 4.5.11).
Когда работающий образец выходит из строя, его непременно отключают, и в работу вступает один из (n – 1) резервных (запасных) элементов. Этот процесс продолжается до тех пор, пока все (n – 1) резервных образцов не будут исчерпаны.
Примем для этой системы следующие допущения:
1. Отказ системы происходит, если откажут все n элементов.
2. Вероятность отказа каждого образца оборудования не зависит от состояния остальных (n – 1) образцов (отказы статистически независимы).
3. Отказывать может только оборудование, находящееся в работе, и условная вероятность отказа в интервале (t, t + dt) равна λ dt; запасное оборудование не может выходить из строя до того, как оно будет включено в работу.
4. Переключающие устройства считаются абсолютно надежными.
5. Все элементы идентичны. Резервные элементы имеют характеристики как новые.

Система способна выполнять требуемые от нее функции, если исправен по крайней мере один из n образцов оборудования. Таким образом, в этом случае надежность равна просто сумме вероятностей состояний системы, исключая состояние отказа, т. е.:

В качестве примера рассмотрим систему, состоящую из двух резервных образцов оборудования, включаемых замещением. Для того чтобы эта система работала, в момент времени t, нужно, чтобы к моменту t были исправны либо оба образца, либо один из двух. Поэтому:

На рис. 4.5.12 показан график функции Р (t) и для сравнения приведен аналогичный график для нерезервированной системы.

ПРИМЕР 4.5.11. Система состоит из двух идентичных устройств, одно из которых функционирует, а другое находится в режиме ненагруженного резерва. Интенсивности отказов обоих устройств постоянны. Кроме того, предполагается, что в начале работы резервное устройство имеет такие же характеристики, как и новое. Требуется вычислить вероятность безотказной работы системы в течение 100 ч при условии, что интенсивности отказов устройств λ = 0,001 ч–1.
Решение. С помощью формулы (4.5.25) получаем:
P (t) = exp(−λ t) ⋅ (1 + λ t).
При заданных значениях t и λ вероятность безотказной работы системы составляет:

Во многих случаях нельзя предполагать, что запасное оборудование не выходит из строя, пока его не включат в работу. Пусть λ1 — интенсивность отказов работающих образцов, а λ2 — резервных или запасных (λ2 > 0). В случае дублированной системы функция надежности имеет вид:

Данный результат для k = 2 можно распространить на случай k = n. Действительно:
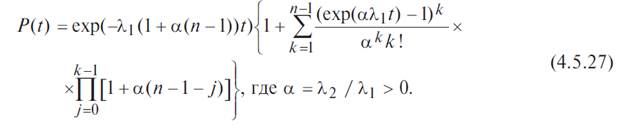
4.5.4.3. Надежность резервированной системы в случае комбинаций отказов и внешних воздействий
В некоторых случаях отказ системы возникает вследствие определенных комбинаций отказов образцов входящих в систему оборудования и (или) из-за внешних воздействий на эту систему. Рассмотрим, например, метеоспутник с двумя передатчиками информации, один из которых является резервным или запасным. Отказ системы (потеря связи со спутником) возникает при выходе из строя двух передатчиков или в тех случаях, когда солнечная активность создает непрерывные помехи радиосвязи. Если интенсивность отказов работающего передатчика равна λ, а φ— ожидаемая интенсивность появления радиопомех, то функция надежности системы:
P (t) = exp(−(λ + ϕ) t) + λ t exp(−(λ + ϕ) t). (4.5.28)
Данный тип модели также применим в случаях, когда резерв по схеме замещения отсутствует. Например, предположим, что нефтепровод подвергается гидравлическим ударам, причем воздействие незначительными гидроударами происходит с интенсивностью λ, а значительными — с интенсивностью φ. Для разрыва сварных швов (из-за накопления повреждений) трубопроводу следует получить n малых гидроударов или один значительный.
Здесь состояние процесса разрушения представляется числом ударов (или повреждений), причем один мощный гидроудар равносилен n малых. Надежность или вероятность того, что трубопровод не будет разрушен действием микроударов к моменту времени t равна:

4.5.4.4. Анализ надежности систем при множественных отказах
Рассмотрим метод анализа надежности нагруженных элементов в случае статистически независимых и зависимых (множественных) отказов. Следует заметить, что этот метод может быть применен и в случае других моделей и распределений вероятностей. При разработке этого метода предполагается, что для каждого элемента системы существует некоторая вероятность появления множественных отказов.
Как известно, множественные отказы действительно существуют, и для их учета в соответствующие формулы вводится параметр α. Этот параметр может быть определен на основе опыта эксплуатации резервированных систем или оборудования и представляет собой долю отказов, вызываемых общей причиной. Другими словами, параметр α можно рассматривать как точечную оценку вероятности того, что отказ некоторого элемента относится к числу множественных отказов. При этом можно считать, что интенсивность отказов элемента имеет две взаимоисключающие составляющие, т. е. λ = λ1 + λ2, где λ1 — постоянная интенсивность статистически независимых отказов элемента; λ2 — интенсивность множественных отказов резервированной системы или элемента. Поскольку α = λ2 / λ, то λ2 = α / λ, и следовательно, λ1 = (1 − α)λ.
Приведем формулы и зависимости для вероятности безотказной работы, интенсивности отказов и средней наработки на отказ в случае систем с параллельным и последовательным соединением элементов, а также систем с k исправными элементами из п и систем, элементы которых соединены по мостиковой схеме.
Система с параллельным соединением элементов (рис. 4.5.13) — обычная параллельная схема, к которой последовательно подсоединен один элемент.

Параллельная часть (I) схемы отображает независимые отказы в любой системе из n элементов, а последовательно соединенный элемент (II) — все множественные отказы системы.
Гипотетический элемент, характеризуемый определенной вероятностью появления множественного отказа, последовательно соединен с элементами, которые характеризуются независимыми отказами. Отказ гипотетического последовательно соединенного элемента (т. е. множественный отказ) приводит к отказу всей системы. Предполагается, что все множественные отказы полностью взаимосвязаны. Вероятность безотказной работы такой системы определяется как Rр = {1 – (1 – R 1) n } R 2, где n — число одинаковых элементов; R 1 — вероятность безотказной работы элементов, обусловленная независимыми отказами; R 2 — вероятность безотказной работы системы, обусловленная множественными отказами.
При постоянных интенсивностях отказов λ1 и λ2 выражение для вероятности безотказной работы принимает вид:

где: t — время.
Влияние множественных отказов на надежность системы с параллельным соединением элементов наглядно демонстрируется с помощью рис. 4.5.14—4.5.16; при увеличении значения параметра α вероятность безотказной работы такой системы уменьшается.
Параметр α принимает значения от 0 до 1. При α = 0 модифицированная параллельная схема ведет себя, как обычная параллельная схема, а при α = 1 она действует как один элемент, т. е. все отказы системы являются множественными. Поскольку интенсивность отказов и среднее время наработки на отказ любой системы можно определить с помощью (4.3.7) и формул:

с учетом выражения для Rр (t) получаем, что интенсивность отказов (рис. 4.5.17) и средняя наработка на отказ модифицированной системы соответственно равны:





ПРИМЕР 4.5.12. Требуется определить вероятность безотказной работы системы, состоящей из двух одинаковых параллельно соединенных элементов, если λ = 0,001 ч–1; α = 0,071; t = 200 ч.
Вероятность безотказной работы системы, состоящей из двух одинаковых параллельно соединенных элементов, для которой характерны множественные отказы, равна 0,95769. Вероятность безотказной работы системы, состоящей из двух параллельно соединенных элементов и характеризуемой только независимыми отказами, равна 0,96714.
Система с k исправными элементами из п одинаковых элементов включает в себя гипотетический элемент, соответствующий множественным отказам и соединенный последовательно с обычной системой типа k из n, для которой характерны независимые отказы. Отказ, отображаемый этим гипотетическим элементом, вызывает отказ всей системы. Вероятность безотказной работы модифицированной системы с k исправными элементами из n можно вычислить по формуле:

где: R 1 — вероятность безотказной работы элемента, для которого характерны независимые отказы;
R2 — вероятность безотказной работы системы с k исправными элементами из n, для которой характерны множественные отказы.
При постоянных интенсивностях λ1 и λ2 полученное выражение принимает вид:

Зависимость вероятности безотказной работы от параметра a для систем с двумя исправными элементами из трех и двумя и тремя исправными элементами из четырех показаны на рис. 4.5.18—4.5.20. При увеличении параметра α вероятность безотказной работы системы уменьшается на небольшую величину (λ t).
Интенсивность отказов системы с k исправными элементами из n и средняя наработка на отказ могут быть определены следующим образом:

где: 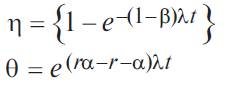
и




ПРИМЕР 4.5.13. Требуется определить вероятность безотказной работы системы с двумя исправными элементами из трех, если λ= 0,0005 ч–1;
Α = 0,3; t = 200 ч.
С помощью выражения для Rkn находим, что вероятность безотказной работы системы, в которой происходили множественные отказы, составляет 0,95772. Отметим, что для системы с независимыми отказами эта вероятность равна 0,97455.
Система с параллельно-последовательным соединением элементов соответствует системе, состоящей из одинаковых элементов, для которых характерны независимые отказы, и ряда ветвей, содержащих воображаемые элементы, для которых характерны множественные отказы. Вероятность безотказной работы модифицированной системы с параллельно-последовательным (смешанным) соединением элементов можно определить с помощью формулы 
где m — число одинаковых элементов в ответвлении, n — число одинаковых ответвлений.
При постоянных интенсивностях отказов λ1 и λ2 это выражение принимает
вид:

Интенсивность отказов системы с параллельно-последовательным соединением элементов и средняя наработка на отказ могут быть определены следующим образом:
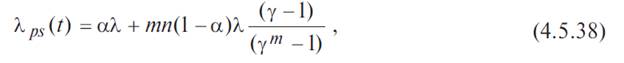

Система, элементы которой соединены по мостиковой схеме, соответствует схеме, состоящей из одинаковых элементов, для которых характерны независимые отказы, и последовательно подсоединенного к ним воображаемого элемента, для которого характерны множественные отказы. При множественном отказе гипотетического элемента вся система выходит из строя.
Вероятность безотказной работы модифицированной системы с элементами, соединенными по мостиковой схеме, можно вычислить по формуле:

(здесь Rb — вероятность безотказной работы мостиковой схемы, для которой характерны множественные отказы). Эта формула при постоянных интенсивностях λ1 и λ2 принимает вид:

(здесь А = (1 – α)λ). Зависимость безотказной работы системы Rb (t) для различных параметров a показана на рис. 4.5.21. При малых значениях λt вероятность безотказной работы системы с элементами, соединенными по мостиковой схеме, убывает с увеличением параметра α.

Интенсивность отказов рассматриваемой системы и средняя наработка на отказ могут быть определены следующим образом:

ПРИМЕР 4.5.14. Требуется вычислить вероятность безотказной работы в течение 200 ч для системы с одинаковыми элементами, соединенными по мостиковой схеме, если λ= 0,0005 ч–1 и α = 0,3.
Используя выражение для Rb (t), находим, что вероятность безотказной работы системы с соединением элементов по мостиковой схеме составляет примерно 0,96; для системы с независимыми отказами (т. е. при α = 0) эта вероятность равна 0,984.
4.5.4.5. Модель надежности системы с множественными отказами
Для анализа надежности системы, состоящей из двух неодинаковых элементов, для которых характерны множественные отказы, рассмотрим такую модель, при построении которой были сделаны следующие допущения и приняты следующие обозначения:
Допущения (1) множественные отказы и отказы других типов статистически независимы; (2) множественные отказы связаны с выходом из строя не менее двух элементов; (3) при отказе одного из нагруженных резервированных элементов отказавший элемент восстанавливается, при отказе обоих элементов восстанавливается вся система; (4) интенсивность множественных отказов и интенсивность восстановлений постоянны.






