Случайная величина — величина, которая в результате опыта может принимать то или иное значение, причем неизвестно заранее какое именно.
Случайная величина может быть дискретной (число отказов за время t, число отказавших элементов при наработке заданного объема и т. д.), либо непрерывной (время наработки элемента до отказа, время восстановления работоспособности).
Закон распределения случайной величины — соотношение, устанавливающее
связь между значения и случайной величины и их вероятностями. Он может быть представлен формулой, таблицей, многоугольником распределений.
Для характеристики случайной величины (непрерывной и дискретной) используется вероятность того, что случайная величина X меньше некоторой текущей переменой x.
Функция распределения случайной величины X (интегральный закон распределения) — функция вида F (x) = p (X < x).
Плотность распределения непрерывной случайной величины X (дифференциальный закон распределения) — производная от функции распределения:

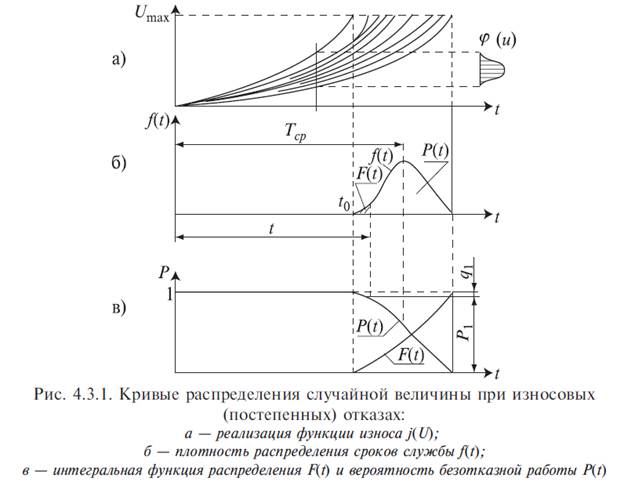
В теории надежности за случайную величину обычно принимают время работы изделия (время до возникновения отказа). В этом случае функция плотности распределения f (t) будет служить полной характеристикой рассеивания сроков службы элементов (рис. 4.3.1). Вид этой функции зависит от закономерностей процесса потери элементом работоспособности.
Кривая распределения f (t) — частота отказов — дает возможность подсчитать средний срок службы элемента Тср (математическое ожидание М [ t ]), рассеивание (дисперсию D) этих сроков службы относительно центра группирования и другие числовые параметры случайной величины Т.
Если взять некоторый период времени работы элемента t, то площадь F (t) кривой распределения f (t) будет характеризовать вероятность отказа (выхода из строя) элемента за этот период времени (рис. 4.3.1, б). Поэтому левая ветвь кривой распределения f (t), относящаяся к области малой вероятности отказов, используется обычно для характеристики безотказности работы изделия, а вся кривая f (t) и ее параметры необходимы для оценки его долговечности.
Ординаты интегральной функции распределения F (t) (рис. 4.3.1, в) характеризуют вероятность отказа детали до данного момента времени:

Во многих случаях нет необходимости пользоваться функциями F (t) или f (t), достаточно знать числовые характеристики этих кривых. Основной характеристикой положения кривой f (t) является математическое ожидание М [ t ], которое в нашем случае является средним сроком службы Тср (наработкой на отказ):

Основной характеристикой рассеивания случайной величины является дисперсия D или среднее квадратическое отклонение σ =√ D:

Чем больше значение D (или соответственно σ), тем больше рассеивание сроков службы относительно их среднего значения М [ t ].
Для оценки надежности работы элемента, принимая за основную случайную величину время до возникновения отказа, можно определить и вероятность безотказной работы P (t) в пределах заданного периода t. Для этого воспользуемся значением интегральной функции:

Вероятность безотказной работы P (t) относится к событию, противоположному появлению отказа F (t). Поэтому F (t) + P (t) = 1 или P (t) = 1 – F (t). Следовательно, P (t) определяется (4.2.5).
В этом случае:
— функция распределения отказа F (t) = P (t < tзад) = Q (t);
— плотность распределения f (t) = dQ (t) / dt;
— вероятность безотказности изделия за время t: P (t) = 1 – Q (t).
Интенсивность отказов (условная плотность вероятности отказов) — отношение f (t) к P (t), см. (4.2.7):


Типичная функция интенсивности отказов изображена на рис. 4.3.2. Участок убывающей интенсивности отказов (t 0 – t 1) иногда называют периодом приработки или периодом ранних отказов. Появление отказов в этом периоде обычно вызывается конструктивными или производственными дефектами.
Участок постоянной интенсивности отказов (t 1 – t 2) называют периодом нормальной эксплуатации. Этот период начинается сразу же после периода приработки и заканчивается непосредственно перед периодом износовых отказов.
Период износовых отказов начинается тогда, когда элемент (устройство) выработал свой ресурс, вследствие чего число отказов в этом периоде начинает возрастать.
Отказы, появляющиеся в периоде нормальной эксплуатации, называют внезапными, так как они появляются в случайные моменты времени, или, другими словами, непредсказуемо.






