Пусть некоторая техническая система D составлена из n элементов (узлов). Допустим, надежности элементов нам известны. Возникает вопрос об определении надежности системы. Она зависит от того, каким образом элементы объединены в систему, какова функция каждого из них и в какой мере исправная работа каждого элемента необходима для работы системы в целом.
Параллельно-последовательная структура надежности сложного изделия дает представление о связи между надежностью изделия и надежностью его элементов. Расчет надежности ведется последовательно — начиная от расчета элементарных узлов структуры к ее все более сложным узлам. Например, в структуре (рис. 4.5.3, а) узел, состоящий из элементов 1—2 — элементарный узел, состоящий из элементов 1—2—3—4 — сложный. Эта структура может быть сведена к эквивалентной, состоящей из элементов 1—2—3—4 и элемента 5, соединенных последовательно. Расчет надежности в данном случае сводится к расчету отдельных участков схемы, состоящих из параллельно и последовательно соединенных элементов.
4.5.3.1. Система с последовательным соединением элементов
Самым простым случаем в расчетном смысле является последовательное соединение элементов системы. В такой системе отказ любого элемента равносилен отказу системы в целом. По аналогии с цепочкой последовательно соединенных проводников, обрыв каждого из которых равносилен размыканию всей цепи, мы и называем такое соединение «последовательным» (рис. 4.5.4).
Следует пояснить, что «последовательным» такое соединение элементов является только в смысле надежности, физически они могут быть соединены как угодно.
С позиции надежности такое соединение означает, что отказ устройства, состоящего из этих элементов, происходит при отказе элемента 1, или элемента 2, или элемента 3, или элемента n. Условие работоспособности можно сформулировать следующим образом: устройство работоспособно, если работоспособен элемент 1, и элемент 2, и элемент 3, и элемент n.
Выразим надежность данной системы через надежности ее элементов. Пусть имеется некоторый промежуток времени (0,τ), в течение которого требуется обеспечить безотказную работу системы. Тогда, если надежность системы характеризуется законом надежности Р (t), нам важно знать значение этой надежности при t = τ, т. е. Р (τ). Это не функция, а определенное число; отбросим аргумент τ и обозначим надежность системы просто Р. Аналогично обозначим надежности отдельных элементов P 1, P 2, P 3,..., P n.
Для безотказной работы простой системы в течение времени τ нужно, чтобы безотказно работал каждый из ее элементов. Обозначим S — событие, состоящее в безотказной работе системы за время; s 1, s 2, s 3,..., s n — события, состоящие в безотказной работе соответствующих элементов. Событие S есть произведение (совмещение) событий s 1, s 2, s 3,..., s n:
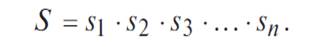
Предположим, что элементы s 1, s 2, s 3,..., s n отказывают независимо друг от друга (или, как говорят применительно к надежности, «независимы по отказам», а совсем кратко: «независимы»). Тогда по правилу умножения вероятностей для независимых событий P (S) = P (s 1) ⋅ P (s 2) ⋅ P (s 3) ⋅... ⋅ P (sn) или в других обозначениях:
а короче:
т. е. надежность (вероятность работоспособного состояния) простой системы, составленной из независимых по отказам, последовательно соединенных элементов, равна произведению надежностей ее элементов.
В частном случае, когда все элементы обладают одинаковой надежностью P 1 = P 2 = P 3 =... = Pn, выражение (4.5.2) принимает вид:
ПРИМЕР 4.5.1. Система состоит из 10 независимых элементов, надежность каждого из которых равна Р =0,95. Определить надежность системы.
По формуле (4.5.3) Р = 0,9510 ≈ 0,6.
Из примера видно, как резко падает надежность системы при увеличении в ней числа элементов. Если число элементов n велико, то для обеспечения хотя бы приемлемой надежности Р системы каждый элемент должен обладать очень высокой надежностью.
Поставим вопрос: какой надежностью Р должен обладать отдельный элемент для того, чтобы система, составленная из n таких элементов, обладала заданной надежностью Р?
Из формулы (4.5.3) получим:
ПРИМЕР 4.5.2. Простая система состоит из 1000 одинаково надежных, независимых элементов. Какой надежностью должен обладать каждый из них для того, чтобы надежность системы была не меньше 0,9?
По формуле (4.5.4)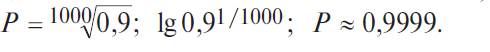 
Интенсивность отказов системы при экспоненциальном законе распределения времени до отказа легко определить из выражения:
λ c = λ1 + λ2 + λ3 +...+λ n, (4.5.5)
т. е. как сумму интенсивностей отказов независимых элементов. Это и естественно, так как для системы, в которой элементы соединены последовательно, отказ элемента равносилен отказу системы, значит все потоки отказов отдельных элементов складываются в один поток отказов системы с интенсивностью, равной сумме интенсивностей отдельных потоков.
Формула (4.5.4) получается из выражения:
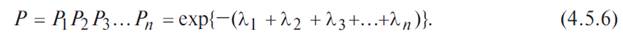
Среднее время работы до отказа:
T 0 = 1 / λ c . (4.5.7)
ПРИМЕР 4.5.3. Простая система S (рис. 4.5.5) состоит из трех независимых элементов, плотности распределения времени безотказной работы которых заданы формулами:
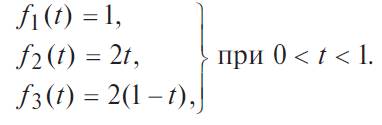
Найти интенсивность отказов системы.
Решение. Определяем ненадежность каждого элемента:
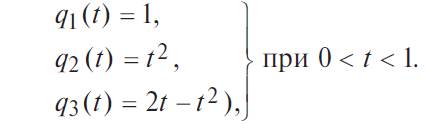
Отсюда надежности элементов:
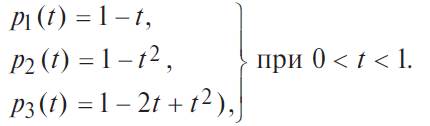
Интенсивности отказов элементов (условная плотность вероятности отказов) — отношение f (t) к p (t):
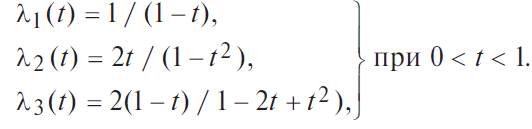
Складывая, имеем: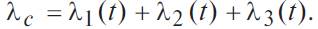 
ПРИМЕР 4.5.4. Предположим, что для работы системы с последовательным соединением элементов при полной нагрузке необходимы два разнотипных насоса, причем насосы имеют постоянные интенсивности отказов, равные соответственно λ1 = 0,0001 ч–1 и λ2 = 0,0002 ч–1. Требуется вычислить среднее время безотказной работы данной системы и вероятность ее безотказной работы в течение 100 ч. Предполагается, что оба насоса начинают работать в момент времени t = 0.
С помощью формулы (4.5.6) находим вероятность безотказной работы P s заданной системы в течение 100 ч:
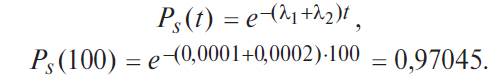
Используя формулу (4.5.7), получаем:
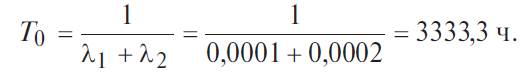
На рис. 4.5.6 представлено параллельное соединение элементов 1, 2, 3. Это означает, что устройство, состоящее из этих элементов, переходит в состояние отказа после отказа всех элементов при условии, что все элементы системы находятся под нагрузкой, а отказы элементов статистически независимы.
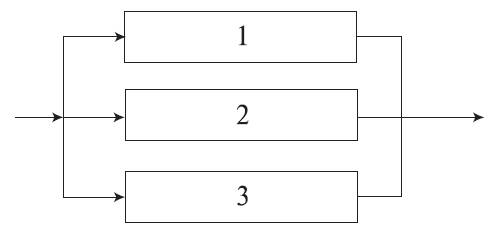
Рис. 4.5.6. Блок-схема системы с параллельным соединением элементов.
Условие работоспособности устройства можно сформулировать следующим образом: устройство работоспособно, если работоспособен элемент 1, или элемент 2, или элемент 3, или элементы 1 и 2, 1 и 3, 2 и 3, 1 и 2 и 3.
Вероятность безотказного состояния устройства, состоящего из n параллельно соединенных элементов определяется по теореме сложения вероятностей совместных случайных событий как
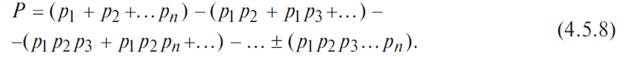
Для приведенной блок-схемы (рис. 4.5.6), состоящей из трех элементов, выражение (4.5.8) можно записать:
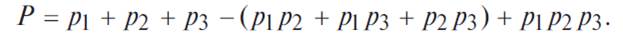
Применительно к проблемам надежности, по правилу умножения вероятностей независимых (в совокупности) событий, надежность устройства из n элементов вычисляется по формуле:
т. е. при параллельном соединении независимых (в смысле надежности) элементов их ненадежности (1 − pi = qi) перемножаются. В частном случае, когда надежности всех элементов одинаковы, формула (4.5.9) принимает вид:
ПРИМЕР 4.5.5. Предохранительное устройство, обеспечивающее безопасность работы системы под давлением, состоит из трех дублирующих друг друга клапанов. Надежность каждого из них р = 0,9. Клапаны независимы в смысле надежности. Найти надежность устройства. Решение. По формуле (4.5.10)
P = 1 − (1 − 0,9)3 = 0,999.
Интенсивность отказов устройства состоящего из n параллельно соединенных элементов, обладающих постоянной интенсивностью отказов λ0, определяется как:
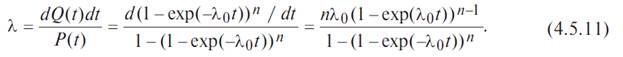
Из (4.5.11) видно, что интенсивность отказов устройства при n > 1 зависит от t: при t = 0 она равна нулю, при увеличении t, монотонно возрастает до λ0.
Если интенсивности отказов элементов постоянны и подчинены показательному закону распределения, то выражение (4.5.9) можно записать:
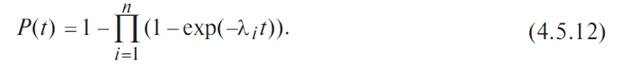
Среднее время безотказной работы системы Т 0 находим, интегрируя уравнение (4.5.12) в интервале [0, ∞]:
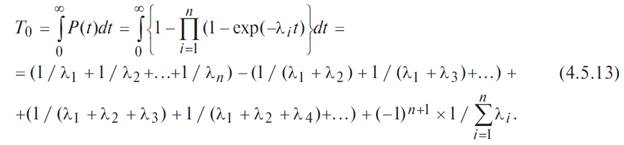
В случае, когда интенсивности отказов всех элементов одинаковы, выражение (4.5.13) принимает вид:
Среднее время работы до отказа также можно получить, интегрируя уравнение (4.5.8) в интервале [0, ∞].
ПРИМЕР 4.5.6. Предположим, что два одинаковых вентилятора в системе очистки отходящих газов работают параллельно, причем если один из них выходит из строя, то другой способен работать при полной системной нагрузке без изменения своих надежностных характеристик.
Требуется найти безотказность системы в течение 400 ч (продолжительность выполнения задания) при условии, что интенсивности отказов двигателей вентиляторов постоянны и равны λ = 0,0005 ч–1, отказы двигателей статистически независимы и оба вентилятора начинают работать в момент времени t = 0.
Решение. В случае идентичных элементов формула (4.5.12) принимает вид:
P (t) = 2exp(−λ t) − exp(−2λ t).
Поскольку λ = 0,0005ч-1 и t = 400 ч, то:
P (400) = 2exp(−0,0005 × 400) − exp(−2 × 0,0005 × 400) = 0,9671.
Среднюю наработку на отказ находим, используя (4.5.13):
T 0 = 1 / λ(1 / 1 + 1 / 2) = 1 / λ × 3 / 2 = 1,5 / 0,0005 = 3000 ч.
4.5.3.3. Способы преобразования сложных структур
Относительная простота расчетов надежности, основанных на использовании параллельно-последовательных структур, делают их самыми распространенными в инженерной практике. Однако не всегда условие работоспособности можно непосредственно представить параллельно-последовательной структурой. В этом случае можно сложную структуру заменить ее эквивалентной параллельно-последовательной структурой. К таким преобразованиям относятся:
— преобразование с эквивалентной заменой треугольника на звезду и обратно;
— разложение сложной структуры по базовому элементу.
Существо способа преобразования с помощью эквивалентной замены треугольника на звезду и обратно заключается в том, что узел сложной конфигурации заменяется на узел другой, более простой конфигурации, но при этом подбираются такие характеристики нового узла, что надежности преобразуемой цепи сохранялись прежними.
Пусть, например, требуется заменить треугольник (рис. 4.5.7, а) звездой (рис. 4.5.7, б) при условии, что вероятность отказа элемента a равна q 13, элемента b равна q 12, элемента c — q 23.
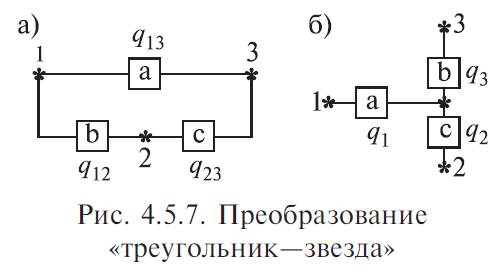
Переход к соединению звездой не должен изменить надежность цепей 1—2, 1—3, 2—3. Поэтому значение вероятностей отказов элементов звезды q 1, q 2, q 3
должны удовлетворять следующим равенствам:
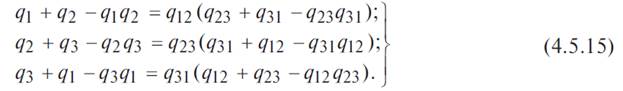
Если пренебречь произведениями вида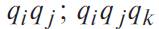 
, то в результате решения системы уравнения (4.5.15) можно записать:
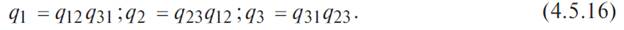
Для обратного преобразования звезды в треугольник:
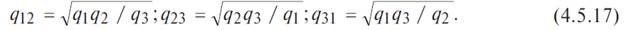
ПРИМЕР 4.5.7. Определить вероятность безотказной работы устройства, структурная схема которого изображена на рис. 4.5.8, б, если известно, что вероятности безотказной работы каждого из элементов схемы равны 0,9, а вероятности отказов равны 0,1.
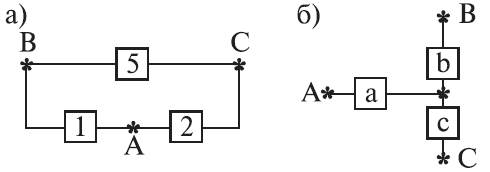
Рис. 4.5.8. К примеру преобразования структуры.
Решение.
1. Преобразуем соединение элементов 1, 2, 5 в треугольник (рис. 4.5.8, а), в звезду (рис. 4.5.8, б).
2. Определим эквивалентные значения вероятности отказов для новых элементов a, b, c:
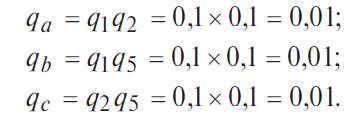
3. Определим значения вероятности безотказного состояния элементов эквивалентной схемы (рис. 4.5.8, б):
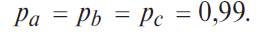
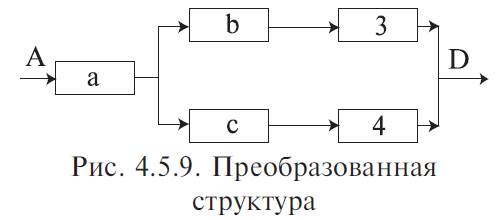
4. Определим вероятность безотказной работы эквивалентного устройства (рис. 4.5.9):
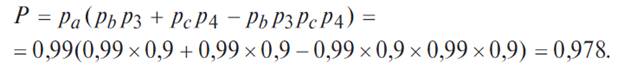
Способ преобразования с помощью разложения сложной структуры по некоторому базовому элементу основан на использовании теоремы о сумме вероятностей несовместных событий. В сложной структуре выбирают базовый элемент (или группу базовых элементов) и делаются следующие допущения:
— базовый элемент находится в работоспособном состоянии;
— базовый элемент находится в отказавшем состоянии.
Для этих случаев, представляющих собой два несовместных события, исходная структура преобразовывается в две новые схемы. В первой из них вместо базового элемента ставится «короткое замыкание» цепи, а во второй — разрыв. Вероятности безотказной работы каждой из полученных простых структур вычисляются и умножаются: первая — на вероятность безотказного состояния базового элемента, вторая — на вероятность отказа базового элемента. Полученные произведения складываются. Сумма равна искомой вероятности безотказной работы сложной структуры.
ПРИМЕР 4.5.8. Решить предыдущий пример методом разложения сложной структуры.
Решение.
1. В качестве базового элемента примем элемент 5 (рис. 4.5.3, б).
2. Закоротим базовый элемент, т. е. сделаем допущение об абсолютной его проводимости. Присоединим к полученной структуре последовательно базовый элемент с характеристикой его надежности р 5. В результате вместо исходной структуры получим новую структуру (рис. 4.5.10, а).
3. Произведем обрыв базового элемента, т. е. сделаем предположение об его абсолютной ненадежности (непроводимости). К полученной структуре присоединим последовательно базовый элемент с характеристикой его ненадежности (1 − p 5). В результате получим структуру (рис. 4.5.10, б).
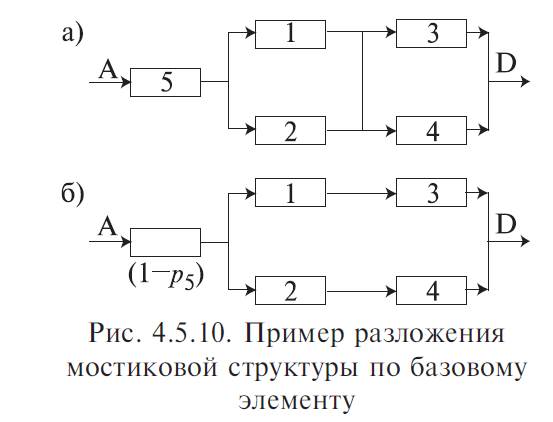
4. Искомая вероятность равна сумме вероятностей структур (рис. 4.5.10, а, б), каждая из которых параллельно-последовательная. Поэтому:
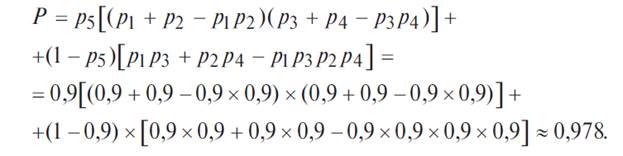
Вероятность безотказной работы мостиковой схемы, состоящей из пяти неодинаковых и независимых элементов, можно определить по формуле:
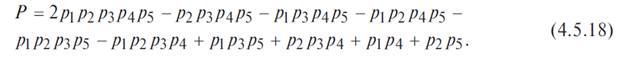
В случае идентичных элементов эта формула принимает вид:
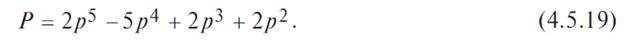
Подставляя соотношение (4.5.19) в формулу (4.5.6), получаем, что в случае использования элементов с постоянной интенсивностью отказов (экспоненциальном законе распределения отказов):
P (t) = 2exp(−5λ t) − 5exp(−4λ t) + 2exp(−3λ t) + 2exp(−2λ t). (4.5.20)
Среднее время безотказной работы системы Т 0 находим путем интегрирования
уравнения (4.5.20) в интервале [0, ∞]:
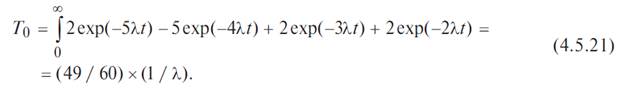
ПРИМЕР 4.5.9. Определить вероятность безотказной работы устройства, структурная схема которого изображена на рис. 4.5.3, б, если известно, что вероятности безотказной работы каждого из элементов схемы равны 0,9.
Решение.
Так как все элементы идентичны, воспользуемся формулой (4.5.18), с ее помощью получаем:
P = 2 × 0,95 − 5 × 0,94 + 2 × 0,93 + 2 × 0,92 ≈ 0,978.
ПРИМЕР 4.5.10. Требуется определить вероятность безотказной работы и среднюю наработку на отказ системы, состоящей из пяти независимых и одинаковых элементов, соединенных по мостиковой схеме (рис. 4.5.3, б); считается, что λ = 0,0005 ч–1, t = 100 ч и все элементы начинают работать в момент времени t = 0.
Решение.
1. С помощью формулы (4.5.20) получаем:
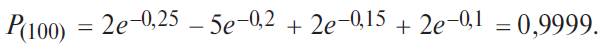
2. Подставляя полученное значение вероятности безотказной работы в формулу (4.5.21), находим среднюю наработку на отказ:
T 0 = 49 / (60 × 0,0005) = 1633,4 ч.
