В общем случае алгоритм МКЭ состоит из четырех этапов.
Этап 1. Выделение конечных элементов (разбиение заданной области на конечные элементы).
Этап 2. Определение аппроксимирующей функциидля каждого элемента (определение функции элемента). На данном этапе значение непрерывной функции j(e) в произвольной точке е- гоконечного элемента аппроксимируется полиномом
, (12)
где А(e) вектор-строка коэффициентов полинома, А0 - свободный член, К = (х,у,г)- вектор координат в рассматриваемой точке. Задачей этого этапа является определение неизвестного вектора А(e) и свободного члена А0.
Для этого, используя условия непрерывности функций в узлах, коэффициенты полинома выражают через вектор f(e) узловых значений функции и координаты узлов и, проделав эквивалентные преобразования, получают
, (13)
где N(e) - матрица-строка, элементы которой называют функциями формы конечного элемента.
Функции формы легко вычисляются в каждой точке конечного элемента через координаты самой точки и координаты узлов элемента. Эту процедуру можно выполнить один раз для типичного элемента. Полученная функция используется далее для всех остальных элементов того же вида (например, треугольных элементов). Эта особенность является важным свойством МКЭ. Благодаря этому элементы с однажды определенными функциями легко включаются в библиотеку конечных элементов. В качестве аппроксимирующих функций используются полиномы (степенные функции).
Рассмотрим алгоритм определения функции элемента для простейшего двумерного симплекс-элемента, представленного на рис.7. Необходимо отметить, что принятая в данном элементе аппроксимация функции j неприменима к задачам расчета пластинок, где у функции прогиба W=j должны быть линейно меняющиеся по координатам х и у вторые производные W”xx, W”yy, W”xy, чтоможно достичь лишь при записи вида
(14)
где ei - индекс, указывающийна принадлежность коэффициента к еi- у элементу - за его пределами 
, что является математическим выражением «финитности» (конечности) данных функций.
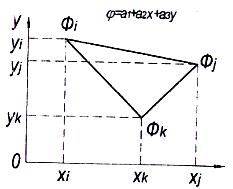
Рис. 7. Функция двухмерного симплекс-элемента
Двухмерный симплекс-элемент, рассматриваемый с упомянутыми выше целями, представляет собой плоский треугольник с прямолинейными сторонами. Интерполяционный полином, аппроксимирующий непрерывную функцию j внутри треугольного симплекс -элемента, имеет вид
(15)
Пронумеруем узлы треугольника i, j, k, двигаясь против часовой стрелки, рис. 7. Узловые значения fi, fj, fk будем считать известными. Используя условие непрерывности искомой функции в узлах, составим систему уравнений
решая которую относительно неизвестных коэффициентов полинома, получим:
(16)
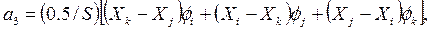
где S — площадь элемента, вычисляемая по формуле
(17)
Поставив (16) в (15) и проделав преобразования, найдем
(18)
где
(19)
и
(20)
Вычисляя значения функций формы Ni, Nj, Nk, нетрудно убедиться, что они равны «1» в узлах с соответствующими номерами и «0» в остальных узлах элемента. Аналогично рассмотренным примерам. вычисляются функции всех прочих типов элементов, набор которых может пополняться в зависимости от типов конструкций, рассчитываемых МКЭ.
Например, для треугольного конечного элемента, рис. 8, в локальной системе координат Xei0eiYei прогиб можно представить в виде полного кубического полинома (14).
Далее, по аналогии с примером, рассмотренным для симплекс-элемгнта, проводятся математические преобразования, в результате чего все 
исключаются и искомыми будут лишь узловые перемещения и их первые производные по обоим ортогональным направлениям. Именно через эти перемещения и их производные осуществляется связь соседних конечных элементов. Заметим, что если узлы попадают на границу тела, то узловые перемещения известны из граничных условий.
Рис.8
Этап 3. Объединение конечных элементов в ансамбль (систему). На этом этапе уравнения (13), относящиеся к отдельным элементам, объединяются в ансамбль, что приводит к системе алгебраических уравнений
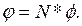(21)
Система (21) является моделью искомой непрерывной функции для всей конструкции.
Основу этого этапа составляет замена произвольно назначенных номеров узлов i, j, k на номера, присвоенные узлам в процессе разбиения рассматриваемой области. Эта процедура приводит к системе линейных алгебраических уравнений, позволяющей при известных узловых значениях искомой функции получить значения последней в любой точке области, занимаемой конструкцией.
Например, на рис.9 треугольная область разбита на элементы треугольной формы.
Рис.9
Пример составления ансамбля конечных элементов для двумерной треугольной области
Соответствие между глобальными и локальными обозначениями узлов будет следующим:
элемент 1 i = 1; j = 2; k = 4;
элемент 2 i = 2; j = 3; k = 5; (22)
элемент 3 i = 2; j = 5; k = 4;
элемент 4 i= 4; j = 5; k = 6.
Подставляя значения (22) в (21), получим
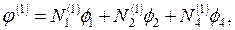
(23)
Аналогично этому замену номеров элементов необходимо проделать в (19) для вычисления функций формы Ni, Nj, Nk. Система уравнений (23) может рассматриваться в качестве сокращенной формы математического описания модели. Расширенная форма имеет вид
(24)
что в матричной форме записывается как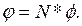
Этап 4. Определение вектора узловых значений функции. В общем случае вектор f неизвестен. Его определение - наиболее сложная процедура в МКЭ. Один из алгоритмов поиска f основан на минимизации функционала, связанного с физическим смыслом задачи. Для задачи расчета пластинки на изгиб минимизируется функционал полной энергии пластинки, представляющий собой сумму потенциальной энергии пластинки и работы внешних сил. Алгоритм состоит из следующих шагов:
Шаг 1. Выбор функционала F, зависящего для стационарных задач, к которым относится и задача изгиба пластинки, от искомой функции j и ее частных производных j'х, j'y, j'г, по вектору пространственных координат:
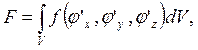(25)
где V - объем конструкции.
Функционал F представляется суммой соответствующих функционалов, относящихся к отдельным конечным элементам
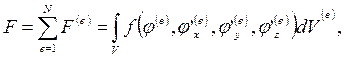(26)
где N - число конечных элементов.
Шаг 2. Подстановка аппроксимирующего выражения (13) в (26) и вычисление производных 
по формулам вида:
(27)
Шаг 3. Минимизация по вектору f функционала F. Для этого составляются уравнения вида
(28)
Суммирование выражений (28) по конечным элементам приводит к получению системы алгебраических уравнений
Кf = Р, (29)
где матрица коэффициентов К называется матрицей жесткости, а Р - вектором нагрузки.
Шаг 4. Решается система уравнений (29), что позволяет определить искомый вектор узловых значений. Найденные значения вектора f подставляются в (21), после чего значения функции j легко вычисляются в любой точке заданной области.
