Суть метода конечных элементов изложим на примере расчета известных задач. Рассмотрим произвольную конструкцию, находящуюся под действием приложенных к ней сил. Конструкция, представляющая собой распределенную систему сложной геометрической формы, рис.4, изображается в виде совокупности конечного количества относительно простых объектов правильной геометрической формы (конечных элементов), рис.5.

Рис. 4. Исходная модель и ее конечно-элементная дискретизация
В качестве таких элементов могут выступать стержни, элементы пластин, многогранники. Конечные элементы, аппроксимирующие исходную конструкцию, считаются связанными между собой в граничных точках (узлах), в каждом из которых вводится несколько степеней свободы, причем их количество зависит от геометрической формы элемента и типа решаемой задачи.
Например, для аппроксимации конструкций стержневыми элементами обычно вводится шесть степеней свободы в узле, рис.6, а, а при моделировании конструкции объемными элементами - по три поступательных перемещения, рис.6, б.

Рис. 5. Примеры конечных элементов
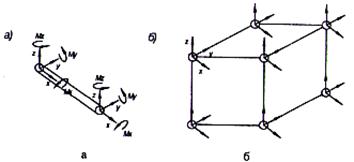
Рис. 6. Стержневой конечный элемент с шестью степенями
свободы в узле (а) и объемный элемент параллелепипеда
с тремя степенями свободы (б) в каждом узле
Действующие на конструкцию внешние нагрузки приводятся к эквивалентным силам (моментам), прикладываемых в узлах конечных элементов. Ограничения на перемещение конструкции (закрепления) также переносятся на конечные элементы, которыми моделируется исходный объект. Поскольку каждый КЭ имеет заранее определенную форму и известны его геометрические характеристики и характеристики материала, то для каждого КЭ, используемого для моделирования конструкции, можно записать систему линейных алгебраических уравнений (СЛАУ) относительно смещений узлов КЭ под действием приложенных в эти узлы сил. Например, для задачи статического анализа конструкций такая система уравнений в матричной форме записывается следующим образом
ККЭ*ХКЭ=РКЭ, (10)
где ККЭ - локальная матрица жесткости конечного элемента, порядок которой равен количеству степеней свободы в узле КЭ,
РКЭ- локальный вектор сил, приложенных к узлам конечного элемента,
ХКЭ - локальный вектор неизвестных узловых перемещений конечного элемента.
Записывая систему (10) для каждого конечного элемента, аппроксимирующего исходную физическую систему, рассматриваем затем их совместно и получаем аналогичную систему уравнений для полной конструкции:
Кг*Хг=Рг, (11)
где Кг- глобальная матрица жесткости конструкции, порядок которой равен произведению количества подвижных узлов конструкции на число степеней свободы в одном узле,
Рг - глобальный вектор сил, приложенных к узлам конечно-элементной дискретизации конструкции,
Хг - глобальный вектор неизвестных узловых перемещений конструкции, подлежащий определению.
Формируя и решая систему уравнений (11), получаем значения перемещений в узлах конечно-элементной сетки, а также напряжения. Эти значения будут приближенными (с позиции теоретически возможного «точного» решения соответствующего дифференциального уравнения (6), но погрешность решения при правильном разбиении конструкции на конечные элементы получается в пределах инженерной точности вычислений. Кроме того, погрешность получаемого в результате конечно-элементной аппроксимации решения обычно плавно уменьшается по мере увеличения степени дискретизации моделируемой системы. Другими словами, чем большее количество КЭ участвует в дискретизации (или чем меньше относительные размеры КЭ), тем точнее получаемое решение.
Отметим, что более плотное разбиение конструкции на КЭ требует более значительных временных затрат ПЭВМ.






