Теоретическая часть. Пластинкой называют тело, имеющее форму прямой призмы высота которого /г значительно меньше размеров основания а и ь

Пластинкой называют тело, имеющее форму прямой призмы высота которого /г значительно меньше размеров основания а и Ь, рис. 1, 2, 3.

а)

Рис.2

б)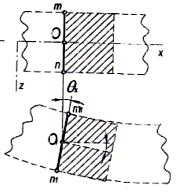

Рис.3

Плоскость, которая делит высоту пластины пополам называет срединной плоскостью. Теория изгиба пластин начинает свое развитие с работ Софи Жермен и Лагранжа.

Теория тонких пластинок построена с использованием следующих гипотез:

1. Считаем, что при изгибе пластинки ее толщина h не изменяется а слои волокон, параллельные срединной плоскости, не давят друг на друга, то есть σ_z=0, e _z=0.

2. Считаем, что всякий прямой элемент, перпендикулярный к срединной плоскости до деформации, остается прямым и перпендикулярным к ней и после деформации, то есть γ_xz=0, γ_yz=0.

3. Считаем срединную плоскость пластинки нерастяжимой, то есть при z=0 имеем U=0, V=0.

При расчете пластинок методом конечных элементов (МКЭ) будем использовать те же допущения. Следовательно, точность получаемых приближенных решений может быть проверена при сопоставлении их с известными решениями технической теории изгиба пластин, основанной на упомянутых допущениях.

Пластинки различают на жесткие (сравнительно толстые), тонкие и мембраны (очень тонкие). Рассмотрим теорию расчета тонких упругих пластинок, для которых справедливы следующие соотношения:

1. Уравнение равновесия:

(1)

где М_x(х,у), М_у(х,у), Н(х,у)- изгибающие и крутящий моменты.

2. Геометрические соотношения (соотношения Коши):

(2)

 

где z - координата по толщине пластинки, W(х,у)- прогиб пластинки, постоянный по ее толщине, e_х, e_у,γ_ху- деформации в произвольной точке пластинки, χ_x, χ_y - деформации в срединной плоскости пластинки, χ- деформация кручения срединной плоскости пластинки.

3. Физические соотношения (закон Гука):

(3)

Интенсивности внутренних силовых факторов (изгибающих и крутящего моментов М_x(х,у), М_у(х,у), Н(х,у)) являются погонными величинами, отнесенными к единице длины сечения пластинки, измеряются в (НМ/М) и подсчитываются по формулам:

(4)

При подстановке в (4) выражений (3) формулы для погонных момен­тов М_х (x, у), M_y(х,у), Н(х,у) принимают вид [1, 2]:

(5)

Подстановкой выражений (5) в (1) получаем уравнение равновесия элемента пластинки (уравнение Софи Жермен):

(6)

Уравнение (6) является неоднородным дифференциальным уравнени­ем четвертого порядка в частных производных. В связи с этим для реше­ния конкретной задачи по каждому направлению в пластинке необходимо задать четыре граничных условия: два на одном и два на другом крае. Рас­смотрим варианты задания граничных условий.

Защемленный край. Если край пластины x= 0 защемлен, то прогиб в точках этого края равен нулю, и заделанное сечение пластины не повора­чивается (плоскость, касательная к изогнутой срединной поверхности, совпадает со срединной плоскостью пластинки до изгиба) [1,2]:

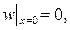
(7)

Условия типа (7) называются геометрическими.

Шарнирно-опертый край. Если край пластины х = 0 шарнирно оперт и может свободно поворачиваться, то прогиб и изгибающий момент на этом крае должны быть равны нулю [1,2]:

В данном случае шарнирные опоры предполагаются жесткими (w= 0) и линия x= 0 остается неизогнутой. Поэтому обращаются в ноль производные:

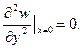
Тогда граничные условия для шарнирно опертого края будут:

(9)

Условия типа (8) называются смешанными (статически геометрическими).

Свободный край. Если край x= 0 свободен от опорных закреплений, то для него обращаются в ноль изгибающие моменты М_х и приведенные поперечные силы Q^*_x (статические граничные условия) [1,2]:

(10)

Переходим к изложению методики решения задач изгиба пластинок, основанной на использовании метода конечных элементов (МКЭ).