Для определения в стержне касательных напряжений 
необходимо иметь эпюры следующих величин:
; 
; 
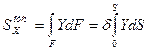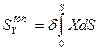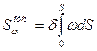(14)
Однако вместо перечисленных величин удобнее использовать величины 
, 
, 
, которые вводятся следующим образом. Рассмотрим безразмерные величины 
, 
, 
, связанные с размерными величинами формулами:
, 
, 
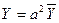(15)
Эпюры , , показаны на рис. 19, 20, 21. Координата 
связана с безразмерной координатой 
соотношениями:
, 
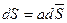(16)
Размеры отдельных частей контура, выраженные через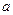 
, приведены на рис.22. Подставляя (15), (16) в (14), получим:
; 
; 
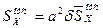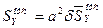(12)
; 
; 
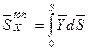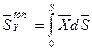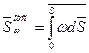(18)
Из выражений (15) видно, что эпюры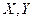 
получаются из , умножением каждой ординаты соответствующей эпюры на 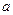, эпюра 
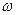- умножением ординат эпюры на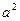 
.
Рассмотрим методику построения эпюр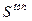 
. На основании выражений (18) эпюра 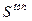представляет собой отложенные в каждой точке значения площади исходной эпюры, заключенной между некоторой начальной точкой и текущей точкой с координатами .
Рис.19 Рис.20
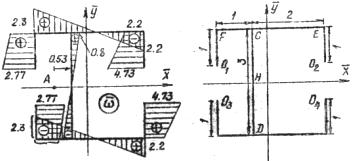
Рис.21 Рис.22
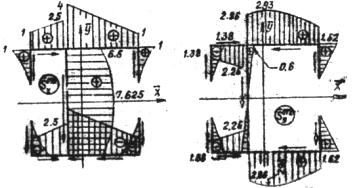
Рис. 32 Рис.24
Помимо значения в каждой точке эпюра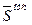 
характеризуется знаком и направлением обхода контура. При смене направления обхода контура меняется знак эпюры и наоборот.
При построении эпюр 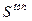рекомендуется придерживаться следующие методики.
Вез свободнее концы контура последовательно рассматриваются в качестве начальных нулевых точек. Обозначим их соответственно через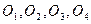 
- рис. 22. На первом этапе рассматриваются части контура, у которых начальными являются указанные точки, а конечными являются точки ветвления контура. Для рассматриваемого контура - это участки 
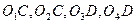. Сами точк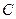и 
и 
, то есть точки ветвления контура, в эти участки не входят.
Дальнейшую последовательность построения эпюр 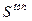подробно проиллюстрируем па примере эпюры .
Рассмотрим часть контура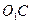 
. На этой части контура выделяем его прямолинейные участки, то есть участки 
и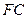 
. При нашем выборе начальных точек направление обхода контура задается однозначно- от точки 
к точке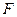 
и от нее- к точке .
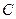Рассмотрим участок . На рассматриваемом участке выберем некоторую точку с координатой . Проведем через эту точку сечение и отбросим ту часть контура, на которую указывает стрелка направления обхода. На рис.26 отбрасываемая часть контура показана штриховой линией. Строим вспомогательную систему координат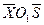 
. В этой системе координат уравнение пряной, ограничивающей эпюру 
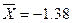. Тогда
(19)
Выражением (19) задается задаётся закон изменения эпюры 
на участке , который представляет собой прямую линию. Для заданной прямой линии достаточно знать значение функции в двух точках. В качестве таких точек естественно выбрать точки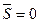 
, 
, 
, 
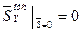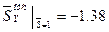. По этим значениям построена эпюра на соответствующем участке - рис. 24.
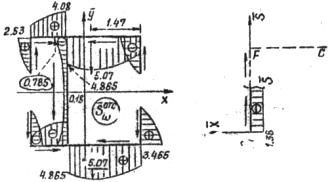
Рис.25 Рис.26
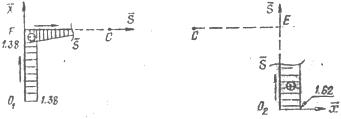
Рис.27 Рис.28
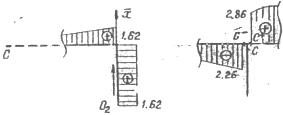
Рис.29 Рис.30
Рис.31 Рис.32
Участок 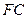, аналогично предыдущему, через некоторую точку участка медленно проводится сечение и отбрасывается та часть контура, на которую. показывает стрелка его обхода - рис.27. Вводится система координат 
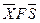. Уравнение прямой, ограничивающей эпюру на участке 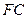, имеет 
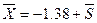. В соответствии с этим получаем:
(20)
Эпюра на участке 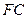изменяется по закону квадратной параболы. Ее значения в точках равны: , , , 
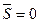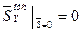. При необходимости подсчитываются ординаты и характерных промежуточных точек.
При построении эпюры на участке 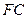учитываем, что в точке 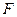уже имеется накопленная с участка величина, равная -1,38.
Рассмотрим часть контура 
.
Участок 
. Вводим систему координат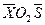 
- рис. 28. Уравнение прямой, ограничивающей эпюру на этом участке, будет 
. Тогда получаем:
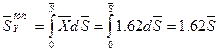(21)
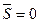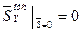При , , при , 
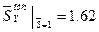
Участок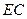 
. Система координат 
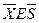изображена на рис.29. Уравнение прямой, ограничивающей эпюру на участке 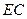, записывается в виде 
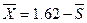, тогда:
(22)
Эпюра на участке 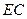изменяется по закону квадратичной параболы, имеет ординаты , ; 
, 
; 
, 
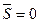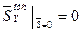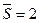. При построении эпюры на участке учитываем, что в точке 
имеется накопленное на участке значение, равное 1.62.
Переходим к определению значения эпюры в точке 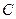ветвления контура. При подходе к точке 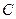слева 
значение эпюры этой точки равно -2,26, при подходе к точке 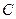справа 
значение эпюры равно 2,86. Требуется определить значение эпюры в точке 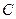неразделенной ветви контура (ее положение показано на рис.30). При переходе к точке 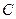отбрасываемые и оставляемые части контура показаны на рис.31. Находим ординату эпюры по формуле:
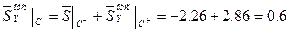
После нахождения значений эпюры 
в точке 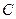эпюра на участке 
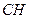строится так же, как и на других участках. Таким образом, значение 
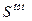в точке ветвления контура определяют так: вначале обрабатывают все ветви контура, имеющие свободные концы, выбирая направление обхода от свободного конца к точке ветвления контура, затем обрабатывают саму точку ветвления контура с последующим выбором направления обхода контура от точки ветвления - рис. 32. При построении эпюры для нижней половины, контура повторяются те же рассуждения, что и для верхней. Окончательный вид эпюры приведен на рис. 24.