МОМЕНТОВ ИНЕРЦИИ 
Для центра тяжести сечения необходимо выполнить следующее:
1. Выбрать исходную систему координат 
(ось Х совпадает с осью симметрии сечения) – рис.3.
Рис.3
2. Разбить поперечное сечение на элементарные части и вычислить площадь всего сечения – рис.3
,
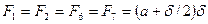
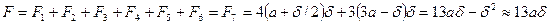
3. Вычислить статические моменты элементарных фигур и всего сечения относительно оси 
. Напомним, что этические моменты некоторой фигуры, относительно оси, вычисляются как произведение площади этой фигуры на расстояние от ее центра тяжести до оси, относительно которой вычисляется статический момент
; 
; 
.
При вычислении площади фигуры F и ее статического момента пренебрегаем членом., содержащим 
, по сравнению с членом, содержащим 
. Тогда
, 
4. Вычислить координаты центра тяжести сечения по формуле
5. Провести через центр тяжести ось ОY и получить систему координат 
, в которой оси 
и 
является главными центральными осями инерции поперечного сечения.
6. Проверить правильность нахождения координат центра тяжести сечения. Известно, что статический момент сечения относительно его центральной оси равен нули. На этом положении основана проверка. Предположим, что ось не проходит через центр тяжести. Вычислим координату центра тяжести 
относительно этой оси. Будем считать, что положению центра тяжести найдено с достаточной точностью, если 
. Используя прежнее разбиение фигуры на элементарные части, получи
Таким образом, положение центра тяжести определено правильно.
Напомним, что статический момент сечения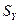 
по определению равен
, (1)
Где 
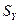. Для вычисления можно непосредственно воспользоваться этим выражением. На рис.4 приведена эпюра 
. Используя при вычислении интеграла правило Верещагина перемножения эпюр (в данном случае одна эпюра - , другая – единая по контуру), получим
Для вычисления величин моментов инерции 
и 
используем формулы 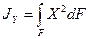/2/
, 
. (2)
С учетом равенства выражения для и примут вид
, 
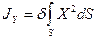. (3)
Эпюры и 
приведены соответственно на рис.4, 5. При вычислении интегралов (3) используется правило Верещагина /2/. Напомним, в чем оно состоит.
Рис.4 Рис.5
Рассматривается интеграл вида 
. В подынтегральное выражение входит произведение функций 
и 
, являющихся ординатой эпюр 
. Для интеграла (1) 
; 
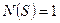. Для интегралов (3): 
, 
: для 
, . Тогда на основании правила Верещагина можно записать
, (4)
где 
- площадь фигуры ограниченной кривой , 
- ордината функций под центром первой фигуры (рис.6). Это правило можно применять только в том случае, если одна или обе эпюры ограничены прямыми. Если одна из эпюр ограничена кривой, то площадь вычисляется той фигуры, которая ограничена кривой. Ордината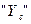 
в этом случае берется обязательно с прямолинейной эпюры. Если обе эпюры ограничены прямыми, то площадь берется любой из них, а ордината - с другой.
Правило Верещагина удобно применять в том случае, когда площадь фигуры и положение ее центра тяжести определяется просто, например, для прямоугольника и треугольника (рис.7, 8), трапеции (рис.9, 10). В последнем случае фигура разбивается на треугольники.
Используя это правило для вычисления интегралов (3), получим
Рис.6 Рис.7
Рис.8
Рис.9
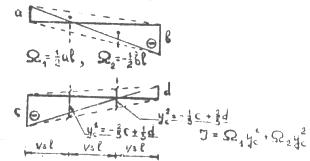
Рис.10
ВЫЧИСЛЕНИЕ 
Участок 1, 2, 6, 7
Участок 3, 4
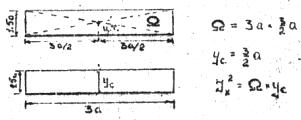
Участок 5
ВЫЯИСЛЕНИЕ
Участок 6, 7
Участок 1, 2
Участок 5
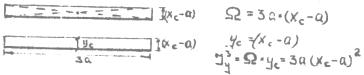
Участок 3, 4 (прямая часть)
Рис.12
Схеме вычислении и приведена соответственно на рис. 11, 12.
Для закрепления пройденного материала рекомендуется проделать самостоятельно аналогичные вькладки для сечения, изображенных на рис. 13, которое соответствует схеме 1 при 
, 
. Затем сравнит их с нижеприведенными.
За исходную выбираем систему координат 
.
, 
, 
,
, 
;
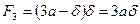
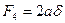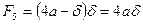
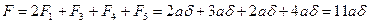
Проводим через центр тяжести ось и получаем систему координат , в которой оси и являются главными центральными осями координат инерции поперечного сечения.
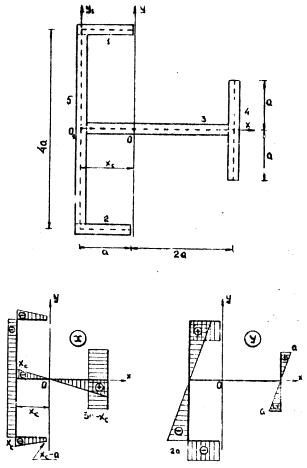
Рис.13
Проверяем правильность положения центра тяжести
Центр тяжести найден верно. Используя правило Верещагина, вычисляем моменты инерции сечения , .
ПОСТРОЕНИЕ ЭПЮР СЕКТОРИАЛЬНЫХ ПЛОЩАДЕЙ,
