На практике нередко встречаются системы, в которых схемы соединения элементов в надежностном смысле не могут быть сведены к последовательно-параллельным. Это системы, содержащие так называемые мостиковые схемы, т.е. системы, содержащие элементы типа треугольник и звезда. Такие схемы встречаются, например, в схемах электрических соединений подстанций и распределительных устройств.
Имеется ряд методов, позволяющих приближенно рассчитывать надежность таких систем. К ним относится метод преобразования треугольника в звезду и обратно. В этом случае в качестве показателей надежности используются вероятности отказов элементов. Выбор указанных характеристик объясняется тем, что метод преобразования треугольника в звезду и обратно является приближенным. Значение возникающей погрешности при оценке надежности системы зависит от вероятностей, характеризующих надежность элементов. Чем меньше эти вероятности, тем меньше погрешность оценки надежности системы. Так как обычно вероятности безотказной работы элементов близки к единице, то целесообразно использовать вероятности появления отказов.
Определим зависимости между вероятностями отказов элементов при преобразованиях, исходя из предположения, что характеристики надежности цепей, соединяющих одноименные точки в различных схемах, должны быть равны между собой.
Вначале рассмотрим точки 1 и 2 (рис. 2.19. и 2.20.). Вероятности отказов для цепей при условии, что точка 3 присоединена к точке 2, будут равны: для звезды 
, а для треугольника 
. Аналогично можно записать равенства и для двух других возможных вариантов соединения точек.
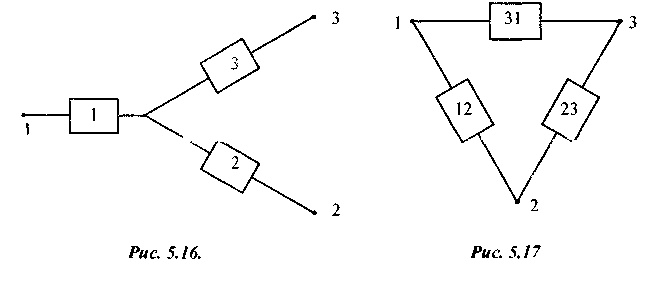
Рис. 2.19. Рис. 2.20.
Таким образом, можно составить следующую систему уравнений:
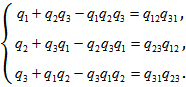(2.73)
Считая, что вероятности отказов элементов малы, и пренебрегая произведениями 
и 
– вероятностями более высокого порядка малости, чем 
, получим следующие приближенные выражения:
; 
; 
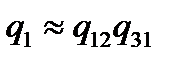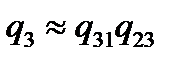. (2.74)
Перемножим соответственно левые и правые части двух первых равенств системы (2.73) и разделим на третье равенство. Тогда
. (2.75)
Из (2.75) после сокращения одинаковых сомножителей имеем
. (2.76)
И аналогично получаем
; 
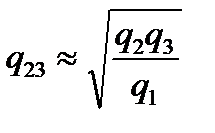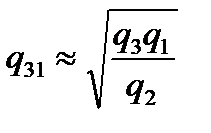. (2.77)
Если предположить, что точка 3 в схеме звезды является свободной, то соответствующие вероятности появления отказов в схемах звезды и треугольника будут соответственно равны для звезды 
; 
; 
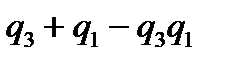, а для треугольника 
; 
; 
.
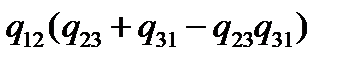Пренебрегая в этих выражениях величинами более высокого порядка малости, чем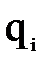 
, (произведения 
), получим следующие приближенные зависимости:
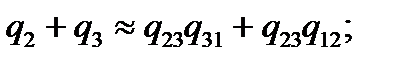(2.78)
Прибавив к левой и правой частям первого уравнения в системе (2.78) соответственно левую и правую части третьего уравнения и вычтя соответственно левую и правую части второго уравнения, получим выражение 
, которое было получено ранее (см. первое уравнение в системе (2.74)). Таким образом, приближенные формулы (2.74), (2.76), (2.77) могут быть использованы в процессе преобразования схемы треугольник в звезду и обратно.
