Будем считать, что резервируемые и резервные элементы равнонадежны, т.е. 
и 
. Для удобства вероятности безотказной работы и появления отказов отдельных элементов обозначаем в этой и последующих главах прописными буквами.
С учетом схемы замещения (рис. 2.8.) и формулы (2.55) вероятность отказа системы с m резервными цепями можно рассчитать следующим образом:
QС = Q0(t) 
, (2.59)
где 
(t) – вероятность отказа основной цепи; 
– вероятность отказа i-й резервной цепи.
Соответственно вероятность безотказной работы системы
(2.60)
Рис. 2.8.
В соответствии с формулой (2.45) имеем
(2.61)
При одинаковых вероятностях отказов основной и резервной цепей 
формулы (2.59) и (2.60) принимают вид:
, (2.62)
. (2.63)
Среднее время безотказной работы системы при общем резервировании
(2.64)
где 
– интенсивность отказов системы; 
– интенсивность отказов любой из (m+1) цепей; 
– интенсивность отказов i -го элемента.
Для системы из двух параллельных цепей (m =1) формула (2.64) принимает вид
(2.65)
Среднее время восстановления системы в общем случае определяется по формуле
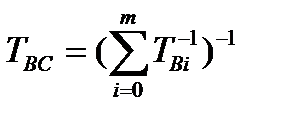, (2.66)
где 
– среднее время восстановления i -й цепи.
Для частного случая m = 1 формула (2.66) принимает вид
(2.67)
Примеры решения задач к разделу 2.3. [ 22 ]
