Последовательным (основным) называется соединение элементов, при котором выход из строя хотя бы одного из них приводит к отказу всей системы, т.е. последовательная структура работоспособна, если все ее элементы работоспособны.
Следует отметить, что в производственной системе элементы физически могут быть соединены и параллельно, однако по надежности они при этом могут соединяться как параллельно, так и последовательно.
Схема замещения (по надежности) системы с последовательной структурой представлена на рис. 2.4.
Рис. 2.4.
Предполагая, что отказы элементов являются независимыми событиями, определяем на основе формулы (2.43) вероятность работоспособности (безотказной работы) последовательной структуры по формуле
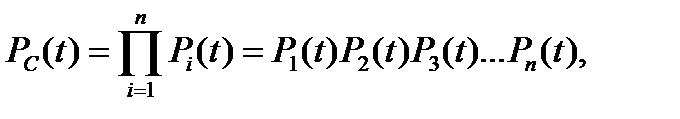(2.44)
где P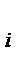 
(t) – вероятность безотказной работы i -го элемента; n – число элементов.
Вероятность отказа последовательной структуры
Qc(t)=1‑Pc(t)=1‑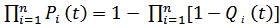 
, (2.45)
где Q 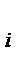– вероятность отказа i -го элемента.
Если все элементы равнонадежны, т.е.
, 
,
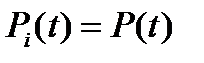то формулы (2.44) и (2.45) принимают вид:
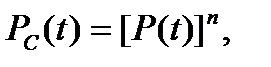(2.46)
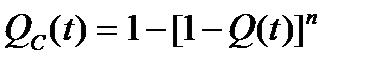. (2.47)
Формулу (2.44) можно представить в общем виде
Pc (t) =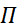 
exp [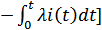 
, (2.48)
где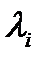 
(t) – интенсивность отказов i -го элемента.
Для экспоненциального закона распределения времени безотказной работы, т.е. при постоянной во времени интенсивности отказов каждого элемента, формула (2.48) упрощается и принимает вид
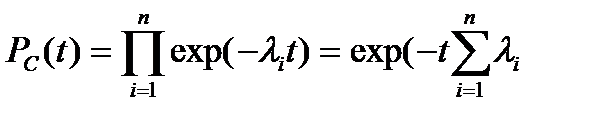). (2.49)
Интенсивность отказов системы с последовательной структурой можно определить по формуле
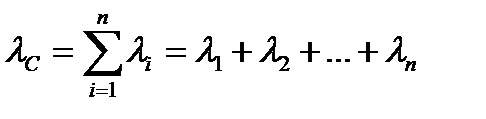. (2.50)
Среднее время безотказной работы системы рассчитывается как
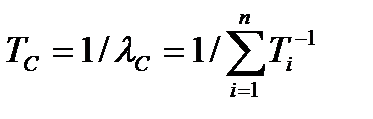, (2.51)
Где Т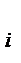 
– среднее время безотказной работы i -го элемента.
Среднее время восстановления системы
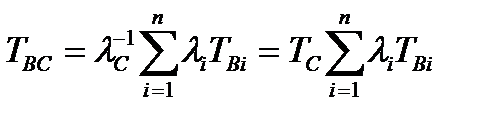, (2.52)
Где Т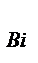 
– время восстановления i -го элемента, является математическим ожиданием времени восстановления, взвешенным по интенсивности отказов n последовательно соединенных элементов.
