Восстанавливаемые объекты – это такие объекты, при эксплуатации которых допускаются многократно повторяющиеся отказы. Эксплуатация таких объектов может быть описана следующим образом: в начальный момент времени объект начинает работу и продолжает работу до первого отказа; после отказа происходит восстановление работоспособности, и объект вновь работает до отказа и т.д. На оси времени моменты отказов образуют поток отказов, а моменты восстановлений − поток восстановлений (рис. 2.2.).
Случайные события, следующие одно за другим в некоторой последовательности, образуют поток случайных событий Поток отказов называется простейшим, если он одновременно обладает тремя свойствами – ординарностью, стационарностью и отсутствием последействия. В ординарном потоке невозможно появление 2‑х и более отказов в один и тот же момент времени. В стационарном потоке вероятность возникновения n отказов в любом промежутке времени Δti зависит только от величины Δti, но не зависит от сдвига Δti по оси времени. В потоке без последействий будущее развитие процесса появления отказов не зависит от того, как этот процесс протекал в прошлом. При решении задач надежности электроснабжения и электрооборудования простейший поток отказов находит широкое применение.
| ||||||||||||
| Рис.2.2. График функционирования восстанавливаемого объекта: t 1… tn − интервалы работоспособности; Δ t 1…Δ tn − интервалы восстановления. |
Процесс функционирования восстанавливаемого объекта можно представить как последовательность чередующихся интервалов работоспособности и восстановления (простоя).
Параметр потока отказов 
− математическое ожидание числа отказов, происшедших за единицу времени, начиная с момента t при условии, что все элементы, вышедшие из строя, заменяются работоспособными, т. е. число наблюдаемых элементов сохраняется одинаковым в процессе эксплуатации. Этот показатель также характеризует восстанавливаемый объект и по статистическим данным определяется с помощью формулы:
,
где n (t 1) и n (t 2) − количество отказов объекта, зафиксированных соответственно, по истечении времени t 1 и t 2.
Если используются данные об отказах по определенному количеству восстанавливаемых объектов, то
, (2.15)
где 
− количество отказов по всем объектам за интервал времени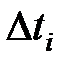 
;
N 0 − количество однотипных объектов, участвующих в эксперименте (отказавший объект восстанавливается, N 0 = соnst).
Для экспоненциального закона надежности интенсивность и параметр потока отказов не зависят от времени и совпадают, т. е.
.
Параметры потока отказов основных элементов электроснабжения приведены в приложении 5.
Вероятность восстановления S (t) − вероятность того, что отказавший элемент будет восстановлен в течение заданного времени t, т. е. вероятность своевременного завершения ремонта.
Очевидно то, что
Для определения величины S (t)используется следующая статистическая оценка:
, (2.16)
где N B(0) − число элементов, поставленных на восстановление в начальный момент времени t = 0;
N B − число элементов, время восстановления которых оказалось меньше заданного времени t, т. е. восстановленных на интервале (0, t).
Вероятность невосстановления (несвоевременного завершения ремонта) G (t)−вероятность того, что отказавший элемент не будет восстановлен в течение заданного времени t.
Статистическая оценка величины G (t):
. (2.17)
| S, Q |
| t |
| S (t) |
| G (t) |
| Рис. 2.3. Графики изменения S (t) и G (t) во времени |
Из анализа выражений (2.16) и (2.17) следует, что всегда
.(2.18)
Частота восстановления а В(t) − производная от вероятности восстановления
. (2.19)
Для численного определения величины а (t)используется статистическая оценка:
, (2.20)
где 
− число восстановленных элементов на интервале времени от t до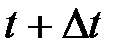 
.
Интенсивность восстановления μ(t) − условная вероятность восстановления после момента t за единицу времени 
при условии, что до момента t восстановления элемента не произошло.
Интенсивность восстановления связана с частотой восстановления:
. (2.21)
Статистически интенсивность восстановления определяется следующим образом:
, (2.22)
, (2.23)
где N ср – среднее количество элементов находящихся в невосстановленом состоянии на интервале времени ∆ t.
Сравнение формул для определения частоты (2.20) и интенсивности (2.22) восстановления показывает, что они отличаются числом элементов в знаменателе. В отличие от процесса отказов, который развивается во времени естественным образом, процесс восстановления является целиком искусственным (ремонт элемента) и, тем самым, полностью определяется организационно-технической деятельностью эксплуатационного персонала. Так как установлены обоснованные нормативы времени на проведение ремонтных работ, то принимают интенсивность восстановления независимой от времени: 
. Численные значения интенсивности восстановления сведены в справочные таблицы по видам оборудования и ремонтов.
Для экспоненциального распределения времени восстановления при постоянной интенсивности восстановления имеем следующие зависимости:
, (2.24)
. (2.25)
Среднее время восстановления Т В представляет собой математическое ожидание времени восстановления и численно соответствует площади под кривой вероятности невосстановления:
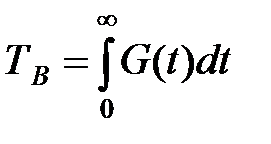. (2.26)
Статистическая оценка величины Т В
,
где ti − наработка между i -1 и i -м отказами, ч; n (t) − суммарное число отказов за время t.
При экспоненциальном распределении времени восстановления, когда интенсивность восстановления μ= const, имеем соотношение
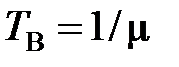, (2.27)
т. е. среднее время восстановления численно равно средней по множеству однотипных элементов (объектов) продолжительности восстановления, приходящейся на один объект. Поскольку 
, то и 
. Численные значения ТВ некоторых элементов электроснабжения приведены в приложении 6.
