Невосстанавливаемым называют такой элемент, который после работы до пер-вого отказа заменяют на такой же элемент, так как его восстановление в условиях экс-плуатации невозможно. В качестве примеров невосстанавливаемых элементов можно назвать диоды, конденсаторы, триоды, микросхемы, гидроклапаны, пиропатроны и т.п.
Пусть время работы невосстанавливаемого элемента представляет собой слу-чайную величину τ. В момент времени t = 0 элемент начинает работать, а в момент t = τ происходит его отказ, следовательно, τ является временем жизни элемента. Таким об-

|


|
|

|
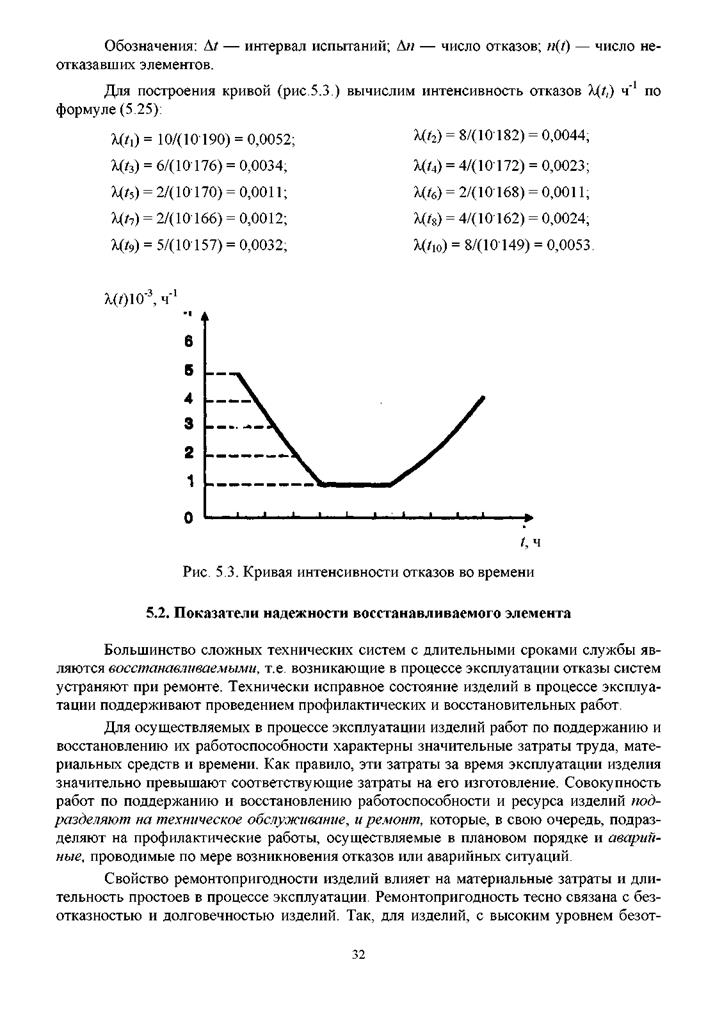
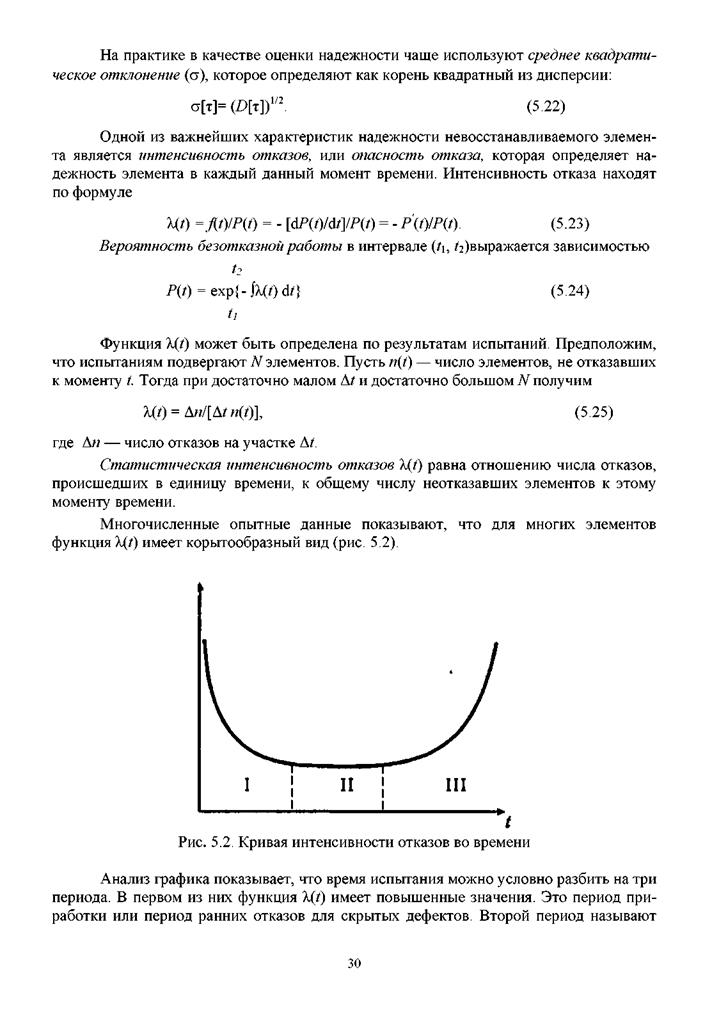
|

|

|

|

|

|
ми и выходными параметрами. При исследовании надежности системы элемент не рас-членяется на составные части, и показатели безотказности и долговечности относятся к элементу в целом. При этом возможно восстановление работоспособности элемента не-зависимо от других частей и элементов системы.
Анализ надежности сложных систем имеет свои специфические особенности. Влияние различных отказов и снижение работоспособности элементов системы по-разному скажутся на надежности всей системы.
При анализе надежности сложной системы все ее элементы и компоненты целе-сообразно разделить на следующие группы.
1) Элементы, отказ которых практически не влияет на работоспособность сис-темы (деформация ограждающего кожуха машины, изменение окраски по-верхности и т.п.). Отказы (т.е. неисправное состояние) этих элементов могут рассматриваться изолированно от системы.
2) Элементы, работоспособность которых за рассматриваемый период времени практически не изменяется (станины и корпусные детали, малонагруженные элементы с большим запасом прочности).
3) Элементы, ремонт или регулировка которых возможна при работе изделия или во время остановок, не влияющих на его эффективность (подналадка и замена режущего инструмента на станке, регулировка холостого хода кар-бюратора автомобильного двигателя).
4) Элементы, отказ которых приводит к отказам системы.
Таким образом, рассмотрению и анализу надежности подлежат лишь элементы последней группы. Как правило, имеется ограниченное число элементов, которые в основном и определяют надежность изделия. Эти элементы и подсистемы выявляются при рассмотрении структурной схемы параметрической надежности.
Модели надежности устанавливают связь между подсистемами (или элемента-ми системы) и их влиянием на работу всей системы. Структурная схема надежности определяет функциональную взаимосвязь между работой подсистем (или элементов) в определенной последовательности. Эту схему составляют по принципу функциональ-ного назначения соответствующих подсистем (или элементов) при выполнении ими определенной части работы, выполняемой системой в целом. Техническая система мо-жет быть сконструирована таким образом, что для успешного ее функционирования необходима исправная работа всех ее элементов. В этом случае ее называют последо-вательной системой. Есть также системы, в которых при отказе одного элемента дру-гой элемент способен выполнить его функции. Такую систему называют параллельной. Очень часто системы обладают свойствами как параллельных, так и последовательных систем — системы со смешанным соединением. При расчете надежности необходимо исследовать действия системы, основываясь на ее функциональной структуре и исполь-зуя вероятностные соотношения.
Такое исследование структуры позволяет выявить узкие места в конструкции системы с точки зрения ее надежности, а на этапе проектирования разработать конст-руктивные меры по устранению подобных узких мест. Например, можно заранее под-считать, сколько резервных элементов необходимо для обеспечения заданного уровня надежности системы. Далее можно рассчитать надежность системы, построенной из элементов с известной надежностью, или наоборот, исходя из требования к надежности системы, предъявить требования к надежности элементов.

|
Сложные системы, состоящие из элементов высокой надежности, могут обла-дать низкой надежностью за счет наличия большого числа элементов. Например, если узел состоит всего из 50 деталей, а вероятность безотказной работы каждой детали за выбранный промежуток времени составляет Pi = 0, 99, то вероятность безотказной ра-боты узла будет P (t) = (0,99)50 = 0,55.
Если же узел с аналогичной безотказностью элементов состоит из 400 деталей, то P (t) = (0,99)400 = 0,018, т.е. узел становится практически неработоспособным.
Пример 6.1. Определить надежность автомобиля (системы) при движении на заданное расстояние, если известны надежности следующих подсистем: системы зажи-гания p 1 = 0,99; системы питания топливом и смазкой p 2 = 0,999; системы охлаждения p 3 = 0,998; двигателя р 4 = 0,995; ходовой части р 5 = 0,997.
Решение. Известно, что отказ любой подсистемы приводит к отказу автомобиля. Для определения надежности автомобиля используем формулу (6.2)
Р = p 1 p 2 p 3 p 4 p 5 = 0,99.0,999.0,998.0,985.0,997 = 0,979. Ответ: Р = 0,979.






