Запишем ранжированный ряд:
190, 200, 200, 200, 200, 200, 210, 210, 210, 220.
Т.к. n = 10, по таблице 2.2 находим число интервалов: k = 4.
Шаг интервала: 
мс.
Примечание: во избежание ошибок при составлении вариационного ряда шаг интервала надо использовать без округлений или округлять только в большую сторону.
Заполним таблицу «Вариационный ряд измерений».
Столбец 1. Записываем порядковые номера интервалов.
Столбец 2. Нижнюю границу 1-го интервала выбираем равной xmin=190; прибавляем шаг интервала: 190 + 7,5 = 197,5 – верхняя граница 1-го интервала (она же нижняя граница 2-го интервала) и т.д.
Столбец 3. Частота интервала равна количеству значений в выборке, которые попали в обозначенный интервал. Первое число включаем в 1-й интервал. Если какое-либо число попало на границу между интервалами, его следует включать в меньший по порядку интервал, например, число на границе 1-го и 2-го интервалов включается в 1-й интервал. Последнее число должно оказаться в последнем интервале. Сумма частот всех интервалов должна быть равна объему выборки.
Вариационный ряд измерений
| № интервала | Границы интервала | Частота |
| 190 – 197,5 | ||
| 197,5 – 205 | ||
| 205 – 212,5 | ||
| 212,5 – 220 |
Полигон распределения
Гистограмма распределения
90 97,5 105 112,5 120
Расчет основных статистических характеристик выборки Б:
| № п/п |  , мс
|  , мс
|  , мс2
|
| 1. | |||
| 2. | |||
| 3. | -13 | ||
| 4. | -3 | ||
| 5. | -33 | ||
| 6. | -13 | ||
| 7. | |||
| 8. | |||
| 9. | -33 | ||
| 10. | -43 | ||
 = 1730 мс
|  = 12210 мс2
|
Запишем выборку Б в порядке возрастания, т.е. ранжированный ряд и найдем моду и медиану.
130, 140, 140, 160, 160, 170, 180, 180, 230, 240.
Мода 1 = 150 мс. Мода 2 = 180 мс.
Медиана = 165 мс.
Среднее арифметическое значение выборки Б:
мс.
Дисперсия:
мс2.
Среднее квадратическое отклонение:
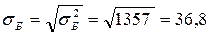мс.
Стандартная ошибка средней арифметической:
мс.
Коэффициент вариации:
.
Размах варьирования R = 240 – 130 = 110 мс
Расчет основных статистических характеристик выборки В:
| № п/п |  , уд.
|  , уд.
|  , уд.2
|
| 1. | |||
| 2. | -4 | ||
| 3. | -33 | ||
| 4. | -28 | ||
| 5. | |||
| 6. | |||
| 7. | |||
| 8. | -2 | ||
| 9. | |||
| 10. | |||
 = 779 уд.
|  = 2991 уд.2
|
Запишем выборку В в порядке возрастания, т.е. ранжированный ряд и найдем моду и медиану.
45, 50, 74, 76, 78, 80, 90, 92, 93, 101.
Моды нет.
Медиана = 79 уд.
Среднее арифметическое значение выборки В:
уд.
Дисперсия:
уд2.
Среднее квадратическое отклонение:
уд.
Стандартная ошибка средней арифметической:
уд.
Коэффициент вариации:
.
Размах варьирования R = 101 – 45 = 56 уд.
Проводя сравнение выборок А, Б и В по их вариабельности, замечаем, что выборка А имеет малый разброс (коэффициент вариации V = 4,1%), выборка Б – большой (V = 21,3%), выборка В – большой (V = 23,3%).
Для оценки репрезентативности выборок А, Б и В рассчитаем величину максимальной ошибки выборок по формуле:
.
Таким образом для выборки А:
мс.
Генеральная средняя будет находиться в диапазоне:
мс или от 193,4 мс до 214,8 мс.
Для выборки Б:
мс.
Генеральная средняя выборки Б будет находиться в диапазоне:
мс или от 126,6 мс до 219,4 мс.
Выборка Б менее репрезентативна, чем выборка А, так как имеет больший интервал генеральной средней.
Для выборки В:
уд.
Генеральная средняя выборки В будет в диапазоне:
уд или от 54,8 уд до 101,2 уд.
Оценим достоверность различий выборок А и Б. Для этого рассчитаем критерий достоверности различий:
.
Так как t > 2, то можно сделать утверждение о достоверности различий выборок А и Б на 95%.
Рассчитаем показатели точности параметров исследуемых выборок:
выборка А: 
;
выборка Б: 
;
выборка В: 
;
Оценивая точность параметров по рассчитанному показателю, отметим, что параметры выборки А являются достаточно точными, потому что CSА < 5 %,а параметры выборок Б и В не являются достаточно точными, так как CSБ и CSВ > 5 %.
