Вернемся теперь к вопросу о случайных событиях. Здесь методически удобнее рассматривать вначале простые события (может произойти или не произойти). Вероятность события X будем обозначать P(X) и иметь ввиду, что вероятность того, что событие не произойдет, составляет
P(X) = 1 - P(X). {2 - 6}
Самое важное при рассмотрении нескольких случайных событий (тем более в сложных системах с развитыми связями между элементами и подсистемами) — это понимание способа определения вероятности одновременного наступления нескольких событий или, короче, — совмещения событий.
Рассмотрим простейший пример двух событий X и Y, вероятности которых составляют P(X) и P(Y). Здесь важен лишь один вопрос — это события независимые или, наоборот взаимозависимые и тогда какова мера связи между ними? Попробуем разобраться в этом вопросе на основании здравого смысла.
Оценим вначале вероятность одновременного наступления двух независимых событий. Элементарные рассуждения приведут нас к выводу: если события независимы, то при 80%-й вероятности X и 20%-й вероятности Y одновременное их наступление имеет вероятность всего лишь 0.8 • 0.2 = 0.16 или 16%.
Итак — вероятность наступления двух независимых событий определяется произведением их вероятностей:
P(XY) = P(X)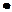 
P(Y). {2 - 7}
Перейдем теперь к событиям зависимым. Будем называть вероятность события X при условии, что событие Y уже произошло условной вероятностью P(X/Y), считая при этом P(X) безусловной или полной вероятностью. Столь же простые рассуждения приводят к так называемой формуле Байеса
P(X/Y) 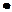P(Y) = P(Y/X) 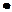P(X) {2 - 8}
где слева и справа записано одно и то же — вероятности одновременного наступления двух "зависимых" или коррелированных событий.
Дополним эту формулу общим выражением безусловной вероятности события X:
P(X) = P(X/Y) 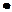P(Y) + P(X/ Y) 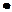P(Y),{2 - 9}
означающей, что данное событие X может произойти либо после того как событие Y произошло, либо после того, как оно не произошло (Y) — третьего не дано!
Формулы Байеса или т. н. байесовский подход к оценке вероятностных связей для простых событий и дискретно распределенных СВ играют решающую роль в теории принятия решений в условиях неопределенности последствий этих решений или в условиях противодействия со стороны природы, или других больших систем (конкуренции). В этих условиях ключевой является стратегия управления, основанная на прогнозе т. н. апостериорной (послеопытной) вероятности события
P(X/Y) 
. {2 - 10}
Прежде всего, еще раз отметим взаимную связь событий X и Y — если одно не зависит от другого, то данная формула обращается в тривиальное тождество. Кстати, это обстоятельство используется при решении задач оценки тесноты связей — корреляционном анализе. Если же взаимосвязь событий имеет место, то формула Байеса позволяет вести управление путем оценки вероятности достижения некоторой цели на основе наблюдений над процессом функционирования системы — путем перерасчета вариантов стратегий с учетом изменившихся представлений, т. е. новых значений вероятностей.
Дело в том, что любая стратегия управления будет строиться на базе определенных представлений о вероятности событий в системе — и на первых шагах эти вероятности будут взяты "из головы" или в лучшем случае из опыта управления другими системами. Но по мере "жизни" системы нельзя упускать из виду возможность "коррекции" управления - использования всего накапливаемого опыта.
