В тех случаях, когда из природы процессов в системе или из данных наблюдений над ней следует вывод о нормальном законе распределения двух СВ - Y и X, из которых одна является независимой, т. е. Y является функцией X, то возникает соблазн определить такую зависимость “формульно”, аналитически.
В случае успеха нам будет намного проще вести системный анализ — особенно для элементов системы типа "вход-выход”. Конечно, наиболее заманчивой является перспектива линейной зависимости типа Y = a + b · X.
Подобная задача носит название задачи регрессионного анализа и предполагает следующий способ решения.
Выдвигается следующая гипотеза:
H0: случайная величина Y при фиксированном значении величины X распределена нормально с математическим ожиданием
My = a + b·X и дисперсией Dy, не зависящей от X. {2 - 14}
При наличии результатов наблюдений над парами Xi и Yi предварительно вычисляются средние значения My и Mx, а затем производится оценка коэффициента b в виде
b = 
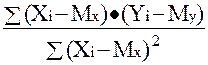= Rxy 
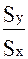{2 - 15}
что следует из определения коэффициента корреляции {2 - 11}.
После этого вычисляется оценка для a в виде
a = My - b MX {2 - 16}
и производится проверка значимости полученных результатов. Таким образом, регрессионный анализ является мощным, хотя и далеко не всегда допустимым расширением корреляционного анализа, решая всё ту же задачу оценки связей в сложной системе.
