Модель Эрланга применяется, как правило, для расчета вероятности потерь при большом количестве источников вызовов и справедлива при таких предположениях:
- вызовы, поступающие на вход системы, образуют пуассоновский (простейший) поток постоянной интенсивности с параметром 
, не зависящим от состояния системы обслуживания 
, т.е. 
;
- длительность занятия подчиняется экспоненциальному распределению с параметром 
, параметр потока освобождений 
;
- вызов, не принятый к обслуживанию в момент поступления, теряется, не влияя на моменты поступления последующих вызовов;
- любой из V выходов пучка доступен, когда он свободен, для любого поступающего вызова;
- исходной для расчета является поступающая нагрузка;
- система находится в стационарном режиме.
Подставляя значения параметров 
и 
в выражение (3.6), получим
,
где 
- интенсивность поступающей нагрузки;
.
На рисунке 3.8 показаны распределения числа занятых каналов в пучке из 5 каналов для различных значений поступающей нагрузки.
Рисунок 3.8 – Распределение числа занятых каналов
в пучке из 5 каналов
Основным показателем качества обслуживания для этой модели является вероятность потерь по времени - средняя доля времени, когда все каналы пучка оказываются занятыми. В этом случае говорят, что в системе наступила блокировка. Вероятность такой блокировки определяется по формуле, носящей в телефонии название В-формулы Эрланга или 1 формулы Эрланга:
.
Для рассматриваемой модели потери по времени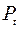 
, по вызовам 
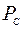и по нагрузке 
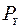совпадают, параметр потерянного потока вызовов - 
, потерянная нагрузка 
.
Прямой расчет формулы Эрланга во многих практических случаях может оказаться затруднительным. Поэтому для расчета часто пользуются рекуррентным соотношением
,
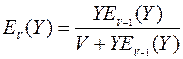последовательно вычисляя 
при начальном значении 
.
Можно запомнить, что , 
, 
.
Действительно
.
На рисунке 3.9 показана зависимость вероятности блокировки от числа каналов пучка и интенсивности поступающей нагрузки.
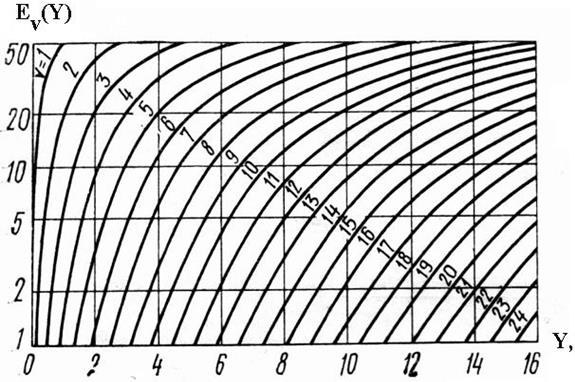
Рисунок 3.9 – Зависимость вероятности блокировки от числа каналов пучка и интенсивности поступающей нагрузки
Далее определим среднее число занятых каналов пучка как
.
Напомним, что среднее число занятых каналов равно интенсивности нагрузки, обслуженной пучком каналов, поэтому можно записать
.
Среднее число свободных каналов пучка определяется как
.
Коэффициент использования выходного канала определяется выражением
.
На рисунке 3.10 показана зависимость коэффициента использования выходного канала от числа каналов пучка и вероятности блокировки.
Рисунок 3.10 –Зависимость коэффициента использования выходного канала от числа каналов пучка и вероятности блокировки
Пример 3.9. Две АТС соединены между собой группой из 24 соединительных линий. Чему равна интенсивность обслуженной нагрузки при вероятности блокировки 0,1? Какова интенсивность поступающей нагрузки при таком значении вероятности блокировки?
Решение. Из рисунка 3.10 следует, что коэффициент использования выходных линий при вероятности блокировки 
, 
должен быть равен 
. Поэтому интенсивность обслуженной нагрузки 
.
Поскольку , то максимальное значение интенсивности поступающей нагрузки будет равно
.
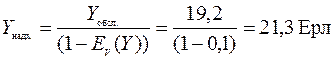Необходимо отметить, что эту задачу можно решить другим способом, применяя формулу Эрланга или графики на рисунке 3.9 для непосредственного нахождения поступающей нагрузки для 24 соединительных линий, а затем определять интенсивность обслуженной нагрузки.
