Розглянемо основні характеристики потоків викликів. Детермінований потік – це потік з фіксованими моментами надходження викликів. Такий потік рідко зустрічається. Якщо моменти надходження викликів залежать від випадкових факторів, то такий потік називається випадковим. Випадковий потік викликів, як послідовність випадкових величин може бути представлений як випадковий процес та заданий трьома еквівалентними засобами:
– послідовністю випадкових моментів часу появи викликів;
– послідовністю випадкових інтервалів часу між викликами;
– послідовністю випадкових чисел, що визначають кількість викликів на заданих інтервалах часу.
Для імовірнісного опису випадкових процесів використовуються такі характеристики:
– функція розподілу моментів часу появи викликів або відповідна їй щільність імовірності;
– функція розподілу інтервалів часу між викликами або відповідна їй щільність імовірності;
– закон розподілу кількості викликів на заданих інтервалах часу.
В зависимости от вида функций распределения потоки вызовов наделяют соответствующими названиями. В общем случае случайные потоки можно классифицировать по наличию или отсутствию трех основных свойств: стационарности, ординарности и последействия.
Потік викликів є стаціонарним, якщо закон розподілу кількості викликів на заданих інтервалах часу 
не залежить від початкового моменту часу 
.
Стаціонарність потоку означає, що імовірність надходження деякої кількості викликів за фіксований інтервал часу залежить тільки від довжини інтервалу і не залежить від його початку. Потік, який не має цієї властивості, є нестаціонарним.
Потік викликів є ординарним, якщо для імовірності надходження двох і більше викликів 
за інтервал часу 
існує межа
.
Ординарність потоку означає неможливість одночасного надходження двох і більше викликів. Потік, який не має цієї властивості, є неординарним.
Потік викликів є потоком без післядії, якщо імовірність надходження викликів за інтервал часу 
, 
не залежить від процесу надходження викликів до моменту .
Зокрема, відсутність післядії означає взаємну незалежність появи кількостей викликів на інтервалах часу, що не перекриваються. Потік, який не має цієї властивості, називається потоком з післядією.
Кількісне описання потоків викликів використовує три основні характеристики:
– провідну функцію потоку 
, що являє собою середню кількість викликів за інтервал часу 
;
– параметр потоку
;
де 
– ймовірність появи хоча б одного виклику на інтервалі часу 
. Т.е. параметр потока есть плотность вероятности поступления вызовов в момент времени t.
– інтенсивність потоку 
являє собою середню кількість викликів, які надходять в одиницю часу в даний момент
.
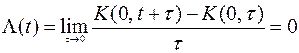Интенсивность потока учитывает возможную неординарность потока, т.е. одновременно поступающие вызовы и определяется как математическое ожидание числа вызовов в единицу времени в данный момент. Для ординарных потоков интенсивность потока равна его параметру.
В общем случае характеристики потоков вызовов зависят от времени. В телефонной сети, например в ночные часы, вызовы возникают редко, а днем наступают периоды повышенной активности абонентов. Тем не менее, большая часть математических моделей теории распределения информации включает в себя так называемые стационарные потоки вызовов, характеристики которых не зависят от времени, так как наиболее часто представляет интерес поведение системы распределения информации в наиболее трудных для нее условиях. В этом случае работа системы рассматривается на относительно небольшом отрезке времени, на протяжении которого параметр потока максимален и существенно не изменяется. В таких условиях поток можно считать стационарным.
У випадку стаціонарних потоків інтенсивність та параметр потоку не залежать від часу. Поскольку число вызовов всегда больше или равно числу моментів поступления этих вызовов (так як викликі можуть надходити одночасно, якщо потік викликів неординарний), справедливо следующее неравенство 
. Для ординарних потоків 
.
Однорідний стаціонарний ординарний потік без післядії називається найпростішим потоком чи стаціонарним пуассонівським потоком.
Пуасонівский (найпростіший) потік викликів. Название потока викликів «пуассоновским» связано с тем, что при условии стационарности, ординарности и отсутствия последействия количество вызовов, попадающих на фиксированный интервал времени, будет распределено по закону Пуассона:
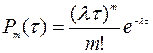, (3.1)
где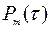 
- вероятность того, что за время 
будет получено ровно 
вызовов.
Проанализируем основные характеристики пуассоновского потока. Из рисунка 3.2 следует, что время как таковое не определяет вероятность появления вызовов, а участвует только в произведении с параметром потока. Поэтому будем использовать безразмерный аргумент 
.
Рисунок 3.2 - Огибающие распределения Пуассона
(пунктир не надо рисовать)
Нетрудно видеть, что зависимость вероятности поступления событий возрастает с увеличением интервала пока 
, а с дальнейшим ростом интервала вероятность убывает и всегда стремится к нулю. Этот факт говорит, что наиболее вероятное число поступивших вызовов за интервал длиной близко к значению 
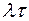. С возрастанием величины огибающие кривые принимают все более симметричный вид, приближаясь к нормальному закону распределения непрерывной случайной величины.
Вероятность того, что за промежуток времени не поступит ни один вызов (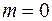
) будет равна
.
Математическое ожидание числа вызовов, попадающих на участок длины , равно
.
Дисперсия пуассоновского распределения равна его математическому ожиданию:
.
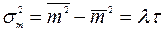А это значит, что число вызовов, поступающих в единицу времени, может колебаться в довольно широких пределах, что соответствует физической природе явления.
Если разделить среднее значение числа вызовов на интервале - 
на длительность этого интервала, то получится как раз интенсивность потока вызовов
.
Таким образом, для пуассоновского потока интенсивность потока равна параметру потока. Отметим, что равенство 
справедливо не только для простейшего потока, но и для любого стационарного ординарного потока.
Зная вероятность наступления заданного числа вызовов в произвольном интервале времени 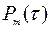, можно найти вероятности наступления не менее вызовов в заданном интервале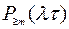 
или вероятность поступления не более вызовов в этом интервале 
:
.
Распределение интервала времени между двумя соседними вызовами. Определим функцию распределения интервала времени 
между двумя соседними вызовами:
.
Для того чтобы выполнялось неравенство 
нужно, чтобы хотя бы один вызов поступил на интервале времени длиной 
(рисунок 3.3).
Рисунок 3.3 – Послідовність викликів, для якої
виконується умова
Вероятность такого события, очевидно, 
, поэтому
. (3.2)
Дифференцируя выражение (3.2), найдем плотность распределения интервала времени между двумя соседними вызовами:
.
Таким образом, мы нашли, что интервал времени между вызовами в пуассоновском потоке заявок имеет экспоненциальное (показательное) распределение. Из этого, разумеется, следует и обратное утверждение: если интервал между соседними вызовами распределен по экспоненциальному закону, то поток вызовов является пуассоновским.
Найдем основные характеристики интервала времени между вызовами для пуассоновского потока. Математическое ожидание интервала времени между вызовами будет равно
,
Дисперсия величины Т равна
,
среднеквадратическое отклонение
.
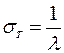Пуассоновские потоки широко применяются в качестве модели реальных потоков благодаря тому, что объединение большого числа независимых стационарных ординарных потоков с последействием при малых значениях параметров этих потоков создает общий поток, близкий к простейшему. Если каждый из потоков поступает от отдельных источников вызовов, то простейший поток можно представить как поток от бесконечного числа источников, параметр каждого из которых стремится к нулю.
Нестаціонарним пуассонівським потоком (найпростішим потоком із змінним параметром) є однорідний ординарний потік без післядії, параметр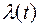 
якого залежить від часу t, а ймовірність появи точно m викликів на інтервалі часу 
визначається формулою
,
де 
.
Під потоком з простою післядією розуміється ординарний потік, для якого у будь-який момент часу t існує кінцевий параметр потоку 
, що залежить тільки від стану S (t)системи обслуговування в цей момент і не залежить від процесу обслуговування заявок до цього моменту. Потік з простою післядією є нестаціонарним, бо його параметр залежить від часу через стан системи, хоча для кожного конкретного стану цей параметр є постійною величиною.
До окремих випадків потоку з простою післядією відносяться симетричний та примітивний потоки.
Симетричним називається потік з простою післядією, параметр якого у будь-який момент часу t залежить тільки від кількості викликів x, що обслуговуються в цей момент, і не залежить від інших характеристик, які визначають стан S (t) системи. Таким чином, 
.
Примітивним називається такий симетричний потік, параметр якого 
прямо пропорційний кількості вільних у даний момент джерел заявок:
,
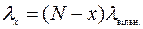де 
– загальна кількість джерел викликів;
– кількість джерел (викликів), які обслуговуються системою;
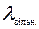– параметр потоку джерела викликів у вільному стані.
Модель примитивного потока удобна для представления потока вызовов от ограниченного числа абонентов. Каждый абонент является источником независимого пуассоновского потока вызовов. Совокупный поток вызовов определяется суммой потоков отдельных абонентов. Однако когда абонент получает обслуживание своего вызова, его поток исчезает из совокупного входного потока, и интенсивность входного потока уменьшается скачком.
Длительность обслуживания одного вызова. В теории распределения информации длительность обслуживания поступающих вызовов обычно принимается либо постоянной, либо случайной величиной.
Постоянная длительность обслуживания. Хотя постоянная длительность обслуживания не характерна для обычного телефонного разговора, это допущение разумно принять для такой деятельности, как обработка заявки на обслуживание вызова, передача цифр телефонного номера, воспроизведение записанных сообщений. Более того, постоянная длительность обслуживания, очевидно, допустима для передачи пакетов фиксированной длины в сетях с коммутацией пакетов.
Случайная длительность обслуживания. Наиболее общее допущение о распределении длительности обслуживания для обычного телефонного разговора - показательное (экспоненциальное) распределение
;
,
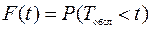где 
- параметр потока обслуживания,
,
- среднее значение длительности обслуживания.
Дифференцируя последнее выражение, найдем плотность распределения длительности обслуживания:
.
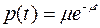Среднее значение времени обслуживания и его дисперсия соответственно равны:
; 
.
Экспоненциальное распределение обладает следующим свойством: вероятность завершения соединения не зависит от того, насколько долго оно продолжалось. Это означает, что независимо от того, как долго продолжается соединение, вероятность того, что t секунд будут последними, определяется как:
.
В этом смысле экспоненциальное распределение длительности обслуживания представляет наиболее ярко выраженный случайный процесс. Даже знание того, как долго длилось обслуживание вызова, не дает информацию о том, когда оно будет окончено.
Поток освобождений. Потоком освобождений называется последовательность моментов окончания обслуживания вызовов. В общем случае свойства и характеристики потока освобождений зависят от поступающего потока вызовов, качества обслуживания этих вызовов, закона распределения длительности обслуживания.
При обслуживании поступающего потока вызовов без потерь при постоянной длительности обслуживания свойства потока освобождений совпадают со свойствами поступающего потока вызовов. Происходит только сдвиг по времени на величину между моментом поступления вызова и моментом окончания его обслуживания.
При показательном законе распределения длительности обслуживания в силу свойства этого распределения моменты окончания обслуживания не зависят от моментов поступления вызовов. В этом случае параметр потока освобождений 
зависит только от параметра показательного закона распределения длительности обслуживания и числа вызовов , которые находятся на обслуживании в системе в данный момент времени:
.
Выражение для параметра потока освобождений можно пояснить тем, что вероятность хотя бы одного освобождения при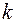 
вызовах, находящихся на обслуживании в системе в 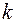раз больше, чем при одном вызове, находящемся на обслуживании в системе. Также можно показать, что в рассматриваемом случае поток освобождений обладает свойством ординарности.
