В системах с восстановлением вышедшие из строя элементы после ремонта вновь включаются в работу. При этом вводится понятие «интенсивность восстановления - μ». Интенсивность восстановления может быть постоянной величиной (мы будем рассматривать именно такую ситуацию), а может зависеть от того, сколько имеется в наличии вышедших из строя элементов. Отказ системы происходит, если все элементы системы вышли из строя, т.е. находятся в ремонте, хотя в конкретный момент времени ремонтируется только один из них.
1. Рассмотрим, так называемый, «теплый» режим работы. В этом режиме рабочий элемент выходит из строя с интенсивностью λ. Остальные элементы также включены, но работают в «облегченном» режиме, при котором вероятность выхода из строя равна λ0.
Естественно, что λ0 << λ.. Целесообразность рассмотрения «теплого» режима связана с тем, что результаты, полученные для этого случая, автоматически обобщаются для двух других, рассмотренных ранее. Достаточно положить λ0 равной нулю, и сразу же получаем формулы для холодного резервирования. При λ0 = λ имеет место горячее резервирование.
Граф подобной системы представлен на рисунке 8.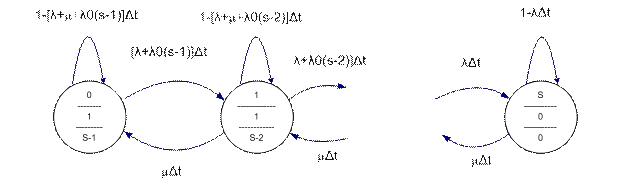 
Рис.8 Граф переходов системы с восстановлением при работе в «теплом режиме».
Уравнения Колмогорова для подобной системы записываются таким образом:
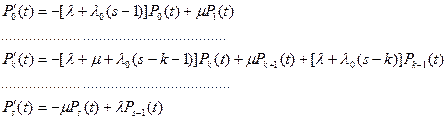(15)
Для систем с восстановлением имеет смысл рассмотреть предельные, т.е. установившиеся вероятности состояний системы. В таких состояниях вероятности становятся постоянными величинами, а производные от них равны нулю. Система дифференциальных уравнений (15) переходит в систему алгебраических уравнений
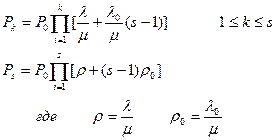(16)
С учетом условия нормировки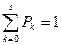 
(условие нормировки заменяет одно
из уравнений системы (16), т.к. эта система линейно зависимых уравнений) получаем окончательные формулы для анализа надежности систем с восстановлением, работающих в облегченном режиме [2]:
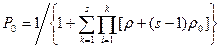(18)
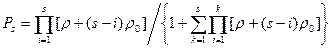(19)
Коэффициент готовности, равный вероятности безотказной работы, для систем с облегченным режимом равен
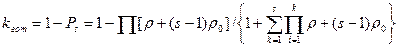(20)
Для систем с холодным резервированием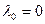 
и. стало быть 
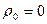, получаем
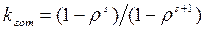(21)
Для систем с горячим резервированием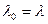 
получаем
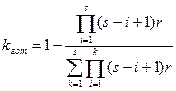(22)
Формулы (21) и (22) являются расчетными для анализа установившихся режимов в системах с восстановлением.
2. Анализ надежности системы с горячим и холодным резервированием методом
имитационного моделирования во многом аналогичен методам, рассмотренным в предыдущей работе. Разница состоит в том, что в нашем случае транзакт, выйдя из канала обслуживания (из многоканального устройства), не покидает систему, а направляется в ремонт. Если прибор, имитирующий механика по ремонту, занят, транзакт становится в очередь. Задержавшись в этом приборе на время ремонта, транзакт блоком TRANSFER вновь возвращается в работу. Второй сегмент GPSS – программы полностью идентичен такому же в ранее рассмотренной программе. Различие состоит только в том, что для получения результатов моделирования необходимо проверку состояния прибора (многоканального устройства) производить через весьма большой интервал времени, когда режим работы системы можно считать установившимся.
