5(I). Связь между f(t), P(t) и или Q(t).
статистическое определение f(t) равно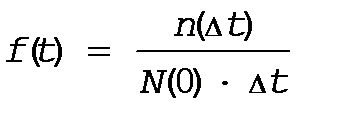 
Рассмотрим f(t) как непрерывную функцию, для этого устремим интервал Dt®0, тогда можно записать
*
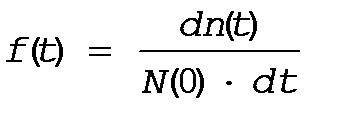Продифференцируем ф-лу (2) статистического определения вероятности безотказной работы
**
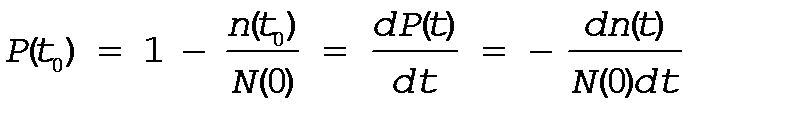Сравним между собой выражения (*) и (**), тогда имеем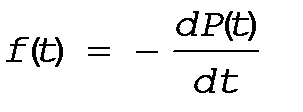 
, (11)
а учитывая что P(t)=1-Q(t) получим 
(12)
27. Связь между показателями надежности λ(t), f(t) и (или) P(t); Q(t).
Связь между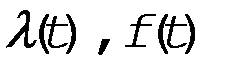 
и P(t) и (или) Q(t)
статистическое определение l(t) имеет вид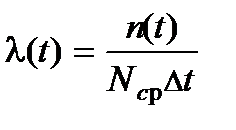 
Рассмотрим теперь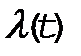 
как непрерывную функцию, для чего устремим 
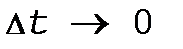, тогда
(*)
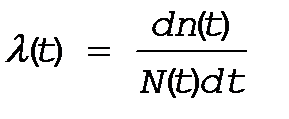Но N(t) можно определить как N(t)=N(0)-N(0)·Q(t)=N(0)·(1-Q(t))=N(0)·P(t) (**)
Подставим значение (**) в (*) получим
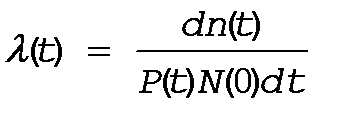(15)
Но очертанная часть выражения (15) - это есть не что иное, как f(t), тогда имеем
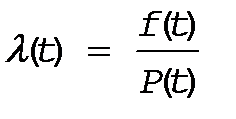(16) или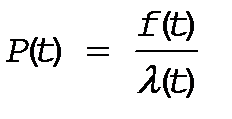 
Из (16) следует что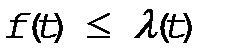 
, т.к. P(t)£ 1
28. Связь между показателями надежности λ(t) и P(t).
Связь между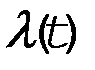 
и P(t)
(**)
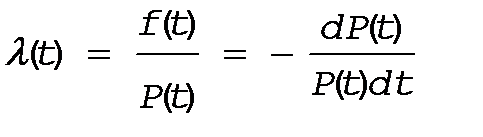Проинтегрируем левую и правую часть выражения (**) в пределах от 0 до t
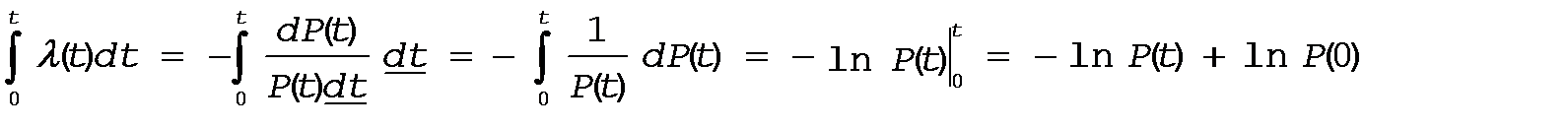
введем обозначение x=P(t), тогда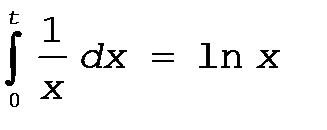 
, но P(0)=1, а ln 1 = 0, (e0=1), тогда
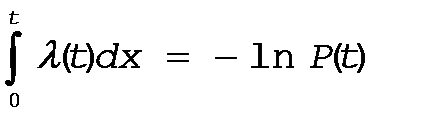или
| Основное выражение в теории надежности 1-ая форма записи основного закона надежности |
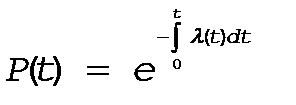(17)
Напомним, вторая форма записи имеет вид
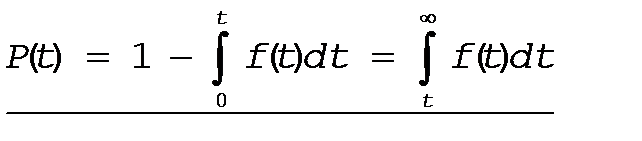
Предположим, что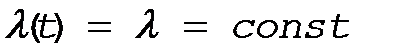 
, тогда из (17) следует
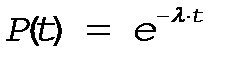(18)
