При суммировании погрешностей руководствуются следующим:
1. Систематические погрешности – 
, если они известны и достаточно точно определены, суммируют алгебраически, т.е. с учетом знаков
(I.43)
2. Случайные погрешности, их среднеквадратические оценки суммируют с учетом их взаимных корреляционных связей, основываясь на известной из теории вероятностей зависимости
(1.44)
где 
– дисперсия суммы двух случайных величин; 
и 
– дисперсии случайных величин; r – коэффициент корреляции между ними, возможные значения которого лежат в интервале от -I до +I.
Суммарная среднеквадратическая погрешность
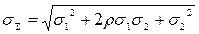(1.45)
Обычно информация о мере корреляционных связей отсутствует, поэтому на практике рассматривают два крайних случая: r=0, r=±1. Если r=0,то случайные погрешности статистически независимы (некоррелированные), и погрешности суммируются геометрически:
где 
– среднеквадратическая оценка погрешности, обусловленной источником.
Если случайные погрешности жёстко коррелированы (r =±1), то между результатами измерений существует функциональная связь. В этом случае они складываются, если r =+1,
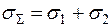(1.46)
или вычитаются, если r =-1
(1.47)
3. Суммирование систематической погрешности со случайной осуществляют с учетом корреляционных связей по тому же принципу, что и суммирование случайных погрешностей.
