Доверительный интервал

Рассмотренные оценки результатов измерений называют точечными. Они указывают интервал значений измеряемой величины, внутри которого находится истинное значение , Поскольку и величины случайные, то возникает вопрос о точности и надежности полученной оценки. Судят об этом по вероятности того, что абсолютное значение отклонения будет оставаться меньше некоторой величины

(1.29)

или

(1.30)

Величина e характеризует точность оценки, а вероятность р, называемая доверительной вероятностью и коэффициентом доверия, – надёжность оценки.

Зависимость (1.30), записанная в виде

(1.31)

говорит о том, что случайный интервал J (p)=2e, находящийся в пределах от , с вероятностью р накрывает величину Q_ист (или неслучайная величина Q_ист с вероятностью p оказывается внутри этого интервала). Интервал J(р) называют доверитель­ным интервалом, а его границы доверительными.

Используя интервальную оценку результатов измерений, необхо­димо задавать доверительный интервал и доверительную вероятность. Если закон распределения вероятностей случайных погрешностей из­вестен, то выбор одной из указанных величин определяет вторую. Это видно из следующего. После подстановки в (1.29) нормированных ве­личин t = D/s и t _p=e/s можно записать известное из теории ве­роятностей равенство

(1.32)

Следовательно, (1.33) и при известной функции распределения F(t) конкретное значение р

определяет значение t _p и наоборот.

В случае нормального распределения и числа наблюдений п³20 t_p выбирается по таблице функций Лапласа (см. табл. 2 приложения), при этом значение вероятности умножается на 2, так как в таблице они приведены для половины симметричного интервала.

Если число наблюдений п £20, доверительный интервал случайной погрешности при заданных вероятности р и средним квадратическим отклонением результата измерения определяется по формуле Стьюдента

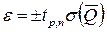(1.34)

где t _p,n - коэффициент распределения Стьюдента, который зависит от заданной вероятности p и числа наблюдений п (табл.3 приложе­ния). При п>20 распределение Стьюдента приближается к нормальному и вместо t _p,n можно использовать t _p для нормального распределе­ния.

При равномерном распределении обычно принимают (т.е. для p=1), поскольку доверительный интервал слабо зависит от доверительной вероятности.

Как правило, в практике измерений доверительную вероятность принимают р = 0.95. Если измерения нельзя повторить, то р =0.99. В особо ответственных случаях, когда проводимые измерения связаны с созданием новых эталонов или от них зависит здоровье людей, то p= 0.997 и выше.

При нормальном законе распределений погрешностей доверитель­ная вероятность р =0.68 соответствует доверительному интервалу

При оценке погрешностей, как уже указывалось, очень важно знать их закон распределения. Из теории вероятностей известно, если имеется большое число наблюдений (п³30), то оказывается возможным проверить гипотезу относительно закона распределения. Гипотеза может быть высказана на основе построения гистограммы. Для проверки соответствия гипотезы экспериментальному распреде­лению существует ряд критериев. Наиболее распространенным является критерий Пирсона, или критерий c²(«хи - квадрат»), который позволяет проверить соответствие экспериментальных данных любому распределению, а не только нормальному.

Схема обработки результатов измерения с многократными наблю­дениями приведена на рис.1.2.