Измеряемая величина, содержащая случайную погрешность, должна рассматриваться как случайная величина. Из теории вероятностей известно, что наиболее полно случайные величины характеризуются законами распределения вероятностей.
Плотность распределения вероятностей
 , (1.13)
, (1.13)
где F(x)– вероятность значений случайной величины х в интервале dx.
Наряду с плотностью распределения вероятностей используется функция распределения вероятностей случайной величины
 , (1.14)
, (1.14)
которая выражает собой вероятность того, что случайная величина находится в интервале от -¥ до x 1. Функция распределения любой случайной величины является неубывающей функцией, определенной так, что F (-¥)=0, а F(+ ¥) = 1. Вероятность того, что случайная величина X примет значение в интервале между x 1 и x 2, равна
 (1.15)
(1.15)
В разнообразных измерительных устройствах законы распределения вероятностей различны. Преимущественно встречаются нормальные и равномерные распределения. Случайная величина X распределена нормально, если её плотность вероятностей имеет вид
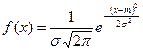 (1.16).
(1.16).
где s - среднее квадратическое отклонение, m =M[Х];
m - математическое ожидание.
Математическое ожидание M[X] случайной величины X является постоянной величиной и характеризует её среднее значение. Величина  является случайной погрешностью. Если систематическая погрешность отсутствует, то математическое ожидание равно истинному значению величины X.
является случайной погрешностью. Если систематическая погрешность отсутствует, то математическое ожидание равно истинному значению величины X.
На рис. I.I, а показана дифференциальная функция нормального распределения f(x). Рассеяние результатов вокруг M[ х ] уменьшаетcя с уменьшением s. При расчетах пользуются нормированным нормальным распределением, когда нормируется случайная величина:
 (1.17)
(1.17)
где  нормированная случайная величина. Интеграл
нормированная случайная величина. Интеграл
 (1.18)
(1.18)

Рис.1.1,а
выражает вероятность попадания случайной погрешности в интервал 0– t 1 и носит название функции Лапласа. Значения f(t) и Р(t 1) приводятся в табл. I и 2 приложения. Из табл. 2 приложения можно найти, что вероятность  появления случайной погрешности в интервалах ± t 1 =
появления случайной погрешности в интервалах ± t 1 =  = ± 1; ±2; ± 3 c учетом симметричности распределения равна соответственно 0,683, 0,954, 0,997. Эти цифры характеризуют вероятность появления случайной погрешности в интервалах ±s'; ±2s;'±3s. Если случайные погрешности определяются по результатам измерений, то в большинстве случаев они имеют нормальное распределение.
= ± 1; ±2; ± 3 c учетом симметричности распределения равна соответственно 0,683, 0,954, 0,997. Эти цифры характеризуют вероятность появления случайной погрешности в интервалах ±s'; ±2s;'±3s. Если случайные погрешности определяются по результатам измерений, то в большинстве случаев они имеют нормальное распределение.
Равномерное распределение, показанное на рис. 1.1,б, записывается в виде:
(1.19)

Вероятность появления погрешности в интервале x 4- x 3 равна

Равномерное распределение имеет погрешность квантования измеряемой величины по уровню в цифровых измерительных приборах.
Если закон распределения неизвестен, то всегда принимают равномерное распределение.
В измерительной практике встречаются и другие законы распределения, которыми в [6] рекомендуется аппроксимировать реальные законы распределений: треугольный, трапециевидный, антимодальные I и II, Рэлея.
Для решения многих задач не требуется знание функции и плотности распределения вероятностей, а вполне достаточными характеристиками случайных погрешностей служат их числовые характеристики: математическое ожидание (первый начальный момент)
 (I.20)
(I.20)
и дисперсия (второй центральный момент)
 (1.21)
(1.21)
Корень квадратный из дисперсии, взятый с положительным знаком, есть среднее квадратическое отклонение случайной величины  .
.
Математическое ожидание является центром группирования случайной величины, а дисперсия характеризует мощность рассеяния.
Нормальное распределение полностью характеризуется математическим ожиданием и дисперсией.
Равномерное распределение (рис I.I,б) тоже определяется двумя параметрами M[ x ]и xт.
Дисперсия равномерного распределения
 (1.22)
(1.22)
а среднее квадратическое отклонение 
Вероятность появления случайной погрешности в интервале ±s составляет р= s/ x m=0.578.
Числовые вероятностные характеристики погрешностей, представляющие собой неслучайные величины, теоретически определяются при бесконечном числе наблюдений. Практически число наблюдений n всегда ограничено. Поэтому реально пользуются статистическими числовыми характеристиками, которые принимают за искомые вероятностные характеристики и называют оценками характеристик. Чтобы подчеркнуть различие между формулами вероятностных характеристик и их оценок, последние отмечают знаком ~.
К оценкам случайной величины, получаемым по статистическим данным, предъявляются требования состоятельности, несмещенности и эффективности.
Оценка параметра Q считается состоятельной, если при увеличении числа наблюдений она стремится к истинному значению оцениваемой величины: 
Несмещенной она называется в том случае, если математическое ожидание её равно истинному значению оцениваемой величины:  .
.
Чем меньше дисперсия оценки, тем более эффективной ее называют  .
.
Обычно для симметричных распределений в качестве оценки математического ожидания ряда равноточных наблюдений принимают среднее арифметическое ряда наблюдений п:
 (1.23)
(1.23)
где q i - результат i наблюдения; п - число наблюдений.
Если отсутствует систематическая погрешность, то при  .
.
Разность  представляет собой случайную погрешность при i -м наблюдении. Она может быть как положительной, так и отрицательной.
представляет собой случайную погрешность при i -м наблюдении. Она может быть как положительной, так и отрицательной.
Среднее арифметическое, независимо от закона распределения, обладает следующими свойствами:
 (I.24)
(I.24)
 (1.25)
(1.25)
Первое свойство используется для проверки правильности вычисления  , а второе положено в основу метода наименьших квадратов.
, а второе положено в основу метода наименьших квадратов.
В качестве оценки дисперсии берётся дисперсия отклонения результата наблюдения
 , (1.26)
, (1.26)
а оценки среднего квадратического отклонения
 . (1.27)
. (1.27)
Формула (1.27) характеризует среднее квадратическое отклонение отдельного наблюдения.
Для вычислений абсолютной погрешности требуется найти разность между результатом наблюдения Qi и истинным значением измеряемой величины Qист. Но Qист никогда неизвестно, поэтому, как уже отмечалось, на практике пользуются действительным значением измеряемой величины. При достаточно большом числе наблюдений, не искаженных систематической погрешностью, в качестве действительного значения можно принять среднее арифметическое результатов наблюдений  и принять его за результат измерения.
и принять его за результат измерения.
Среднее арифметическое  зависит от числа наблюдений и является случайной величиной с некоторой дисперсией относительно истинного значения величины Qист , т.е. величину
зависит от числа наблюдений и является случайной величиной с некоторой дисперсией относительно истинного значения величины Qист , т.е. величину  можно рассматривать как оценку Qист, т.е.
можно рассматривать как оценку Qист, т.е.  .
.
В теории вероятностей показывается, что оценкой дисперсии среднего арифметического ряда наблюдений относительно истинного значения является
 (1.28)
(1.28)
Величину  называют средним квадратическим отклонением результата измерений.
называют средним квадратическим отклонением результата измерений.
Следовательно, взяв за результат измерения  , уменьшаем среднее квадратическое отклонение в
, уменьшаем среднее квадратическое отклонение в  раз по сравнению со случаем, когда за результат измерения принимается любое одно из п наблюдений. Из полученных выражений видно, что многократные измерения с последующим усреднением результатов позволяют уменьшить случайную составляющую погрешности, а также оценить её.
раз по сравнению со случаем, когда за результат измерения принимается любое одно из п наблюдений. Из полученных выражений видно, что многократные измерения с последующим усреднением результатов позволяют уменьшить случайную составляющую погрешности, а также оценить её.
 , (1.13)
, (1.13) , (1.14)
, (1.14) (1.15)
(1.15)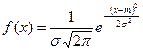 (1.16).
(1.16). является случайной погрешностью. Если систематическая погрешность отсутствует, то математическое ожидание равно истинному значению величины X.
является случайной погрешностью. Если систематическая погрешность отсутствует, то математическое ожидание равно истинному значению величины X. (1.17)
(1.17) нормированная случайная величина. Интеграл
нормированная случайная величина. Интеграл (1.18)
(1.18)
 появления случайной погрешности в интервалах ± t 1 =
появления случайной погрешности в интервалах ± t 1 =  = ± 1; ±2; ± 3 c учетом симметричности распределения равна соответственно 0,683, 0,954, 0,997. Эти цифры характеризуют вероятность появления случайной погрешности в интервалах ±s'; ±2s;'±3s. Если случайные погрешности определяются по результатам измерений, то в большинстве случаев они имеют нормальное распределение.
= ± 1; ±2; ± 3 c учетом симметричности распределения равна соответственно 0,683, 0,954, 0,997. Эти цифры характеризуют вероятность появления случайной погрешности в интервалах ±s'; ±2s;'±3s. Если случайные погрешности определяются по результатам измерений, то в большинстве случаев они имеют нормальное распределение.







 (I.20)
(I.20) (1.21)
(1.21) .
. (1.22)
(1.22)

 .
. .
. (1.23)
(1.23) .
. представляет собой случайную погрешность при i -м наблюдении. Она может быть как положительной, так и отрицательной.
представляет собой случайную погрешность при i -м наблюдении. Она может быть как положительной, так и отрицательной. (I.24)
(I.24) (1.25)
(1.25) , а второе положено в основу метода наименьших квадратов.
, а второе положено в основу метода наименьших квадратов. , (1.26)
, (1.26) . (1.27)
. (1.27) и принять его за результат измерения.
и принять его за результат измерения. зависит от числа наблюдений и является случайной величиной с некоторой дисперсией относительно истинного значения величины Qист , т.е. величину
зависит от числа наблюдений и является случайной величиной с некоторой дисперсией относительно истинного значения величины Qист , т.е. величину  можно рассматривать как оценку Qист, т.е.
можно рассматривать как оценку Qист, т.е.  .
. (1.28)
(1.28) называют средним квадратическим отклонением результата измерений.
называют средним квадратическим отклонением результата измерений. , уменьшаем среднее квадратическое отклонение в
, уменьшаем среднее квадратическое отклонение в  раз по сравнению со случаем, когда за результат измерения принимается любое одно из п наблюдений. Из полученных выражений видно, что многократные измерения с последующим усреднением результатов позволяют уменьшить случайную составляющую погрешности, а также оценить её.
раз по сравнению со случаем, когда за результат измерения принимается любое одно из п наблюдений. Из полученных выражений видно, что многократные измерения с последующим усреднением результатов позволяют уменьшить случайную составляющую погрешности, а также оценить её.





