Обработку экспериментальных данных при функциональном преобразовании результатов измерений целесообразно осуществлять по алгоритму [1, с. 144 – 166]. При этом необходимо учитывать, что n = 12, следовательно, порядок расчетов и их содержание определяются условием 10...15 < n < 40...50.
1. Обработать результаты измерений величин X и У отдельно по алгоритму, изложенному в п. п. 1-3 задания 2, при этом:
– определить оценки результатов измерений X, У и средних квадратических отклонений Sx, Sy;
– обнаружить и исключить ошибки;
– проверить гипотезу о нормальности распределения оставшихся результатов измерений.
2. Определить оценку среднего значения функции:
 .
.
3. Определить поправку:
 .
.
Таблица 3 – Исходные данные
| Последняя цифра шифра | Z=f (X,Y) | Характер и единицы величин | ||
| X | Y | Z | ||
| Z = X/Y | напряжение, мВ | сила тока, мкА | сопротивление | |
| Z = X 2 Y | сила тока, мкА | сопротивление, Ом | мощность | |
| Z =2 X / Y 2 | перемещение, м | время, мс | ускорение | |
| Z =2 m / X∙Y | индуктивность, мкГн | емкость, мкФ | период колебаний | |
| Z =3 X /4p ∙Y 3 | масса, мкг | радиус сферы, мкм | плотность материала | |
| Z = X∙Y 2/2 | индуктивность, мкГн | сила тока, мА | энергия магнитного поля | |
| Z =0,5 X 2/ Y | заряд, пКл | емкость, пФ | энергия конденсатора | |
| Z = X ∙ Y /(X + Y) | сопротивление, Ом | сопротивление, Ом | сопротивление | |
| Z = X /(Y +10) | ЭДС, мВ | сопротивление, Ом | сила тока | |
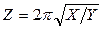
| масса, г | жесткость, Н/м | период колебаний |
4. Определить оценку стандартного отклонения функции
 ,
,
где nx , ny – числа оставшихся результатов измерений, соответственно, X и У после исключения ошибок.
5. Определить доверительный интервал для функции
ЕZ = t × S.
Если законы распределения вероятности результатов измерения X и У признаны нормальными, то t можно определить для принятой доверительной вероятности Р из таблиц для распределения Стьюдента (таблица 1.1.2.8 [2] или таблица Д.1). При этом число степеней свободы m определятся из выражения
 .
.
Если гипотеза о нормальности распределения результатов измерения X или (и) У отвергается, то t целесообразно определить из неравенства Чебышева:
 .
.






