Порядок расчета

Результат многократного измерения находится по алгоритму, представленному на рисунке 40 [1]. При этом необходимо учитывать, что n = 24, следовательно, порядок расчетов и их содержание определяются условием 10…15 < n < 40…50.

1. Определить точечные оценки результата измерения: среднего арифметического 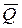и среднего квадратического отклонения S_Q результата измерения.

2. Обнаружить и исключить ошибки. Для этого необходимо:

– вычислить наибольшее по абсолютному значению нормированное отклонение

 

;

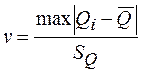– задаться доверительной вероятностью Р и из соответствующих таблиц (таблица П.6 [3] или из таблица В.1) с учетом q = 1 – Р найти соответствующее ей теоретическое (табличное) значение ν_q;

– сравнить ν с ν_q.

Если ν > ν_q, то данный результат измерения Q_i является оши­бочным, он должен быть отброшен. После этого необходимо повторить вычисления по пунктам 1 и 2 для сокращенной серии результатов изме­рений. Вычисления проводятся до тех пор, пока не будет выполнять­ся условие ν < ν_q.

3. Проверить гипотезу о нормальности распределения оставших­ся результатов измерений.

Проверка выполняется по составному критерию [3].

Применив критерий 1, следует:

– вычислить отношение

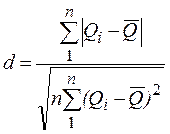
– задаться доверительной вероятностью P ₁ (рекомендуется принять P ₁ = 0,98) и для уровня значимости q ₁ = 1 – Р ₁ по соответствующим таблицам (таблица П.7 [3] или таблица Г.1) определить квантили рас­пределения d _{1-0,5 q l},и d _{0,5 q 1};

– сравнить d с d _{1-0,5 q l} и d _{0,5 q 1}.

Если d _{1-0,5 q 1} < d < d _{0,5 q 1}, то гипотеза о нормальном законе распределения вероятности результата измерения согласуется с экспериментальными данными.

Применив критерий 2, следует:

– задаться доверительной вероятностью Р ₂ (рекомендуется принять Р ₂ = 0,98) и для уровня значимости q ₂ = 1 – Р ₂ с учетом n опреде­лить по соответствующим таблицам (таблица П.8 [3] или таблица Г.2) зна­чения m и Р *;

– для вероятности Р * из таблиц для интегральной функции нормиро­ванного нормального распределения Ф (t) (таблица 1.1.2.6.2 [2] или таблица Б.1) определить значение t и рассчитать Е = t ∙ S_Q.

Если не более m разностей | 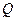_i - | превосходит Е, то гипо­теза о нормальном законе распределения вероятности результата из­мерения согласуется с экспериментальными данными, закон можно признать нормальным с вероятностью Р ₀ ³ (Р ₁ + Р ₂ – 1).

Если хотя бы один из критериев не соблюдается, то гипотезу о нормальности распределения отвергают.

4. Определить стандартное отклонение среднего арифметическо­го.

Если закон распределения вероятности результата измерений признан нормальным, то стандартное отклонение определяют как .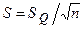

Если гипотеза о нормальности распределения отвергает­ся, то

 

.

 

5. Определить доверительный интервал.

Если закон распределения вероятности результата измерений признан нормальным, то доверительный интервал для заданной дове­рительной вероятности Р определяется из распределения Стьюдента Е = t × S, где t выбирается из соответствующих таблиц (таблица 1.1.2.8 [2] или таблица Д.1, при этом m = n – 1, а a = Р).

Если гипотеза о нормальности распределения отвергается, то t определяется из неравенства П. Л. Чебышева:

 

Р ³ 1 – 1/ t ².