Таблица 1 – Результаты наблюдений
| n | ||||||||||||
| А, мВ | 20,5 | 19,5 | 19,5 | 20,5 | 20,5 | 19,5 | 20,5 | 20,5 | 20,5 | 20,5 |
| 19,5 | 19,5 | 19,5 | 19,5 | 20,5 | 19,5 | 20,5 | 19,5 | 19,5 | 20,5 |
Статистическую обработку результатов наблюдений (таблица 1) выполняли по ГОСТ 8.207-76 для доверительной вероятности Р=0,95 /1/.
Вычисление среднего арифметического исправленных результатов наблюдений, принимаемое за результат измерения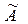 
.
,
где xi- i-й результат наблюдения.
(мВ)
Вычисление оценки среднего квадратического отклонения (СКО) результата наблюдения
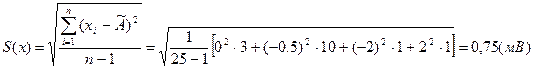
Среднее квадратичное отклонение 
результата измерения оцениваем по формуле
Проверка гипотезы о том, что результаты наблюдений принадлежат нормальному распределению, производим по составному критерию.
Критерий 1.
Вычисляем отношение 
где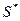 
- суммарная оценка СКО, вычисляемая по формуле
.
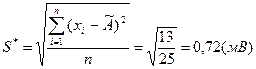Первый критерий удовлетворяется, если
,
где 
и 
- квантили распределения, получаемые из таблицы ГОСТ 8.207-76 по данным n, q1/2 и (100-q1/2), причем q1 – заранее выбранный уровень значимости: q1/2 = 5%, 100-q1/2=95%.
Т.к. 0,7337 < 
=0,77<0,8637, то первый критерий удовлетворяется.
Критерий 2.
Можно считать, что критерий 2 удовлетворятся, если не более m разностей 
превзошли значение 
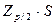. Здесь S – оценка СКО результата наблюдения, 
- верхняя квантиль распределения нормированной функции Лапласа, отвечающая вероятности Р/2. Значение m выбирают из таблицы в зависимости от числа наблюдений n=25 и принятого уровня значимости q2=5%. В данном случае m=2.
Анализ показывает, что только две разности (18-20) и (22-20), равные 2 превзошли 1,47.
Итак, оба критерия соблюдаются и распределение результатов наблюдений соответствует нормальному закону.
Для исключения грубых погрешностей из результатов наблюдений строим возрастающий вариационный ряд чисел:
18£19,5£19,5£19,5£19,5£19,5£19,5£19,5£19,5£19,5£19,5£20£20£20£20,5£20,5£20,5£20,5£20,5£20,5£20,5£20,5£20,5£20,5£22.
Крайние числа проверяем на анормальность. Критерием анормальности служит соотношение между
и 
где х1 и хn – первый и последний члены ряда, и значением b, которое для данного n и принятой вероятности a=1-Р(un³b) берут из таблицы.
Т.к. 
и 
,
то результаты наблюдений 18 мВ и 22 мВ не являются анормальными.
Доверительные границы e (без учета знака) случайной погрешности результата находим по формуле
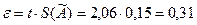(мВ)
Доверительные границы неисключенной систематической погрешности результата измерения принимаем q = ± 0,5 мВ (0,5 деления шкалы осциллографа дефектоскопа).
Т.к. отношение 
, т.е. 0,8<3.33<8, то границу погрешностей результата измерения вычисляем по формуле
, где 
,
а коэффициент
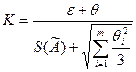, причем 
Если Р=0,95, то К=1,1.
Тогда абсолютная погрешность результатов измерения
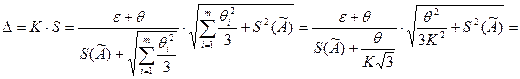
(мВ).
Результат измерения: (20,0±1,1)мВ; Р=0,95; n=25.
