Обработка результатов косвенных измерений

 

Пусть x₁, x₂,..., x_n - величины, измеренные прямыми методами. Тогда, если измеряемая величина X является функцией от x₁, x₂,..., x_n, то есть X = F (x₁, x₂,..., x_n), то измерение считают косвенным. Погрешность определения величины

X зависит не только от погрешности измерения величин x_i, но и от вида функциональной зависимости F.

Рассмотрим два случая косвенных измерений, отличающихся подходами при оценке их погрешности.

Случай 1. Измеряемые аргументы не взаимосвязаны.

Оценку истинного значения измеряемой величины производят по формуле

, (3.1)

где x₁, x₂,..., x_i - среднее значение аргументов, получаемое по результатам прямых измерений.

Оценку абсолютной погрешности косвенного измерения производят по формуле

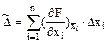. (3.2)

Составляющую погрешности вычисляют по формуле

. (3.3)

Оценку среднего квадратического отклонения составляющих результирующей погрешности определяют из соотношения

, (3.4)

где - оценки среднего квадратического отклонения случайной погрешности результата измерения отдельных x_i.

Оценка СКО результата измерения

. (3.5)

Границы интервала, в котором с заданной вероятностью находится случайная погрешность результата измерения,

, (3.6)

где - квантильный множитель распределения итогового результата косвенного измерения, соответствующий доверительной вероятности P.

Если число измерений не менее 20, t_p определяется из таблиц нормированного нормального распределения; если же число прямых

измерений меньше 20, то можно воспользоваться распределением Стьюдента с эффективным числом степеней свободы

, (3.7)

где n_i - число прямых измерений величины x_i.

. (3.8)

 

В качестве 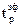можно выбрать квантильный множитель распределения Стьюдента, число измерений которого соответствует минимальному числу произведенных измерений.

Если имеются систематические погрешности D_ci прямо измеряемых величин x_i, то общую систематическую погрешность D_c вычисляют по формуле

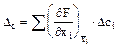. (3.9)

Ее исключают из результата измерения введением поправки (-D_c).

Граница неисключенной систематической погрешности результата косвенного измерения вычисляется по формуле

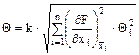, (3.10)

где k - коэффициент, определяемый принятой доверительной вероятностью. При P = 0,95 k = 1,1.

Суммарную погрешность результата косвенного измерения определяют согласно ГОСТ 8.207 - 76 в зависимости от соотношения и , как и для прямых измерений.

Случай 2. Измеряемые аргументы взаимосвязаны (коррелированы) и различие между результатами определяется как погрешностями измерений, так и теснотой связи измеряемых аргументов.

Оценка дисперсии результата косвенных измерений определяется по формуле

(3.11)

где r_ij - коэффициент корреляции погрешностей измерения величин x_i и x_j, учитывающий тесноту зависимости между ними.

Возможные значения коэффициента корреляции лежат в интервале . Если , то погрешности некоррелированы. Равенство свидетельствует о наличии функциональной (а не вероятностной) зависимости.

Оценку коэффициента корреляции производят по формуле

, (3.12)

где m - наименьшее из чисел наблюдений за величинами x_i и x_j.

Пример

Произвести оценку суммарной погрешности косвенного измерения мощности по результатам 5 прямых измерений тока и напряжения. Предел основной относительной погрешности амперметра составляет 1%, вольтметра - 2%. Результаты наблюдений представлены в таблице 2 и принадлежат нормальному распределению.

Таблица 2 - Результат измерений

Номер измерения
U, В	10,2	10,1	10,1	10,3	9,9
I, А	2,4	2,2	2,3	2,4	2,3

 

1 Проверки крайних значений возрастающих вариационных рядов U и I показали, что они не являются анормальными.

2 Вычисляем средние арифметические значения U и I.

= 10,12 В; = 2,32 А.

3 Определим среднюю мощность по результатам измерения U и I.

=22,26 Вт.

4 Оцениваем квадрат СКО результатов измерения напряжения и тока.

=440×10^-5 В²,

= 140×10^-5 А².

5 Вычислим квадраты частных производных мощности по напряжению и току.

= 5,38 А²,

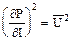= 102,41 В².

6 Произведем оценку среднего квадратического отклонения результата измерения мощности.

7 Вычислим доверительный интервал случайной погрешности, соответствующий P = 0,95.

Вт.

8 Определим доверительные границы неисключенной систематической погрешности результата измерения. В качестве границ НСП измерения тока и напряжения принимаем пределы допускаемых погрешностей применяемых средств измерений: для вольтметра - 2%, для амперметра - 1%.

В.

A.

 

9 Определим суммарную погрешность результата измерения D.

Так как , то есть 0,8 < 1,39 < 8, то границы абсолютной погрешности результата измерения D (без учета знака) определяют по более сложной формуле

 

 

 

 

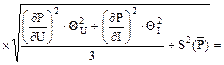
10 Результат измерения:

P = (22,26 ±1,19) Вт, P = 0,95.