При статистической обработке группы результатов наблюдений следует выполнить следующие операции /1/.
2.1 Исключить известные систематические погрешности из результатов наблюдений.
2.2 Вычислить среднее арифметическое исправленных результатов наблюдений, принимаемое за результат измерения 
.
. (2.1)
2.3 Вычислить оценку среднего квадратического отклонения (СКО) результата наблюдения
, (2.2)
где xi – i-й результат наблюдения;
n – число результатов наблюдений.
2.4 Среднее квадратическое отклонение 
результата измерения оценивают по формуле
. (2.3)
2.5 Проверить гипотезу о том, что результаты наблюдений принадлежат нормальному распределению (см. приложение А). Проверку этой гипотезы проводить с уровнем значимости q от 10 до 2%. Конкретные значения уровней значимости должны быть указаны в методике выполнения измерений.
При n>50 для проверки принадлежности результатов наблюдений к нормальному распределению по ГОСТ 11.006–74 предпочтительным является один из критериев: c2 Пирсона или w2 Мизеса-Смирнова. Если 15<n<50, то предпочтительным является составной критерий (приложение А). При 
принадлежность результатов наблюдений к нормальному распределению не проверяют. При этом нахождение доверительных границ случайной погрешности по методике, предусмотренной ГОСТ 8.207–76, возможно в том случае, если заранее известно, что результаты наблюдения принадлежат нормальному распределению.
2.6 Если результаты наблюдений удовлетворяют нормальному закону распределения, то грубые погрешности исключают в соответствии со стандартом. Так, при известном среднем квадратическом отклонении sn критерием анормальности служит соотношение между 
или 
и значением b, которое для данного n и принятой вероятности (уровня значимости) 
берут из таблицы В.1 (приложение В). Если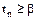 
, то результат х1 (или хn) анормальный. При неизвестном sn критерием анормальности служит соотношение между 
или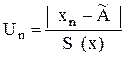 
и значением b, которое для данного n и принятой вероятности 
берут из таблицы В.2 (приложение В). Если 
, то результат х1 (или хn) отбрасывается как анормальный. В этом случае заново вычисляют результат измерения и оценку СКО результата измерения.
2.7 Доверительные границы e (без учета знака) случайной погрешности результата измерения находят по формуле
, (2.4)
где t – коэффициент Стьюдента, который в зависимости от доверительной вероятности Ри числа результатов наблюдений n находят по таблице справочного приложения Б.1.Доверительную вероятность Р принимают равной 0,95, допускается указывать границы для доверительной вероятности Р=0,99. В
особых случаях, например при измерениях, результаты которых имеют значение для здоровья людей, допускается вместо Р=0,99 принимать более высокую доверительную вероятность.
2.8 Вычислить границы неисключенной систематической погрешности (неисключенных остатков систематической погрешности) результата измерения (НСП).
Неисключенная систематическая погрешность результата измерения образуется из составляющих, в качестве которых могут быть неисключенные систематические погрешности: метода; средств измерения; вызванные другими источниками. Границами составляющих НСП принимают, например, пределы допускаемых основных и дополнительных погрешностей средств измерений, если случайные составляющие погрешности пренебрежимо малы.
При суммировании составляющих НСП результата измерения НСП средств измерения каждого типа и погрешности поправок рассматривают как случайные величины. Если данные о виде распределения случайных величин отсутствуют, то их распределения принимают за равномерные. При равномерном распределении НСП их границы (без учета знака) вычисляют по формуле
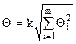, (2.5)
где Qi – граница i-й неисключенной систематической погрешности
к– коэффициент, определяемый принятой доверительной вероятностью. Коэффициент k принимают равным 1,1 при доверительной вероятности Р=0,95.
При доверительной вероятности Р=0,99 коэффициент k принимают равным 1,4, если число суммируемых неисключенных систематических погрешностей более четырех (m>4). Если же число суммируемых погрешностей равно четырем или менее четырех, то значение k определяют по графику (ГОСТ 8.207-76).
Доверительную вероятность для вычисления границ неисключенной систематической погрешности принимают той же, что и при вычислении доверительных границ случайной погрешности результата измерения.
2.9 Вычисление доверительных границ погрешности результата измерения.
Если отношение 
, то неисключенными систематическими погрешностями по сравнению со случайными пренебрегают и принимают, что граница погрешности результата D=e. Если 
, то случайной погрешностью по сравнению с систематическими пренебрегают и принимают, что границы погрешности результата D=Q. Погрешность, возникающая из-за пренебрежения одной из составляющих погрешности результата измерения при выполнении указанных неравенств, не превышает 15%.
Если представленные выше неравенства не выполняются, то допускается границы погрешности результата измерения D (без учета знака) вычислять по формуле
, (2.6)
где K – коэффициент, зависящий от соотношения случайной и неисключенной систематической погрешностей;
SS – оценка суммарного среднего квадратического отклонения результата измерения.
При этом SS вычисляют по формуле 
, а коэффициент
. (2.7)
2.10 Форма записи результатов измерений.
Оформление результатов измерений производят по ГОСТ 8.011-72.
2.10.1 При симметричной доверительной погрешности результаты измерений представляют в форме
, (2.8)
где – результат измерения.
Числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и погрешности D.
2.10.2 При отсутствии данных о виде функций распределений составляющих погрешности результата и необходимости дальнейшей обработки результатов или анализа погрешностей результаты измерений представляют в форме: 
.
2.11 Правила округления
1 Погрешность результата измерения указывается двумя значащими цифрами (все цифры, стоящие справа после нулей), если первая из них равна 1 или 2, и одной, если первая есть 3 и более. Округление производится лишь в окончательном ответе, а все предварительные расчеты выполняются не менее чем с одним-двумя лишними знаками.
Пример.
Произвести оценку результата измерения постоянного тока с помощью амперметра, имеющего предел основной приведенной погрешности 1%. Шкала применяемого прибора равномерная. Нулевая отметка находится на краю шкалы. Конечное значение диапазона измерения – 200А. Определить результат и погрешность измерения, считая распределение нормальным.
Таблица 1 – Результаты измерений
| Номер измерения | |||||
| I, A |
1 Среднее арифметическое результата измерения
.
2) Оценка среднего квадратического отклонения результата измерения производится по формуле
3 Доверительная граница случайной погрешности результата измерения
.
4 В качестве доверительной границы неисключенной систематической погрешности результата измерения принимаем предел допускаемой абсолютной погрешности амперметра
.
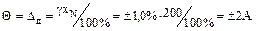Т.к. 
, т.е. 0,8<4<8, то границу погрешностей результата измерения вычисляем по формуле 
. Причем 
.
.
5 Результат измерения (101,4 ± 2,5) А, Р=0,95.
