Основы метрологии и стандартизации
Методические указания
к практическим занятиям для студентов специальности 1-54.01.02 «Методы и приборы контроля качества и диагностика состояния объектов».
Могилев 2005
УДК 389:65.012.23(075). Составитель проф. Новиков В. А.
Основы метрологии и стандартизации. Методические указания к практическим занятиям.–Могилев: Белорусско-Российский университет, 2005.–22с.
Методические указания разработаны в соответствии с рабочей программой по дисциплине “Основы метрологии и стандартизации” для студентов специальности 1-54.01.02 «Методы и приборы контроля качества и диагностика состояния объектов». В работе рассмотрены основные методы обработки результатов измерений, приведены примеры решения типовых задач, даны задачи для практических занятий.
Одобрено на заседании кафедры “Физические методы контроля” Белорусско-Российского университета
“__”_ июня_2005 г., протокол №__
Рецензент доц. В. Ф. Поздняков
Редактор Л. В. Авдевич
Рекомендовано к опубликованию комиссией методического совета Белорусско-Российского университета
Ответственный за выпуск Новиков В. А.
Основы метрологии и стандартизации
ã Составление В. А. Новиков, 2005
Подписано в печать _______. Формат 60х84 1/16. Бумага офсетная. Печать трафаретная.
Усл. печ. л..Уч.-изд. Л..Тираж экз. Заказ № ________.
Издатель и полиграфическое исполнение:
Белорусско-Российский университет
Лицензия ЛВ №243 от 22.02.2001 г, лицензия ЛП №165 от 22.02.2001 г.
212005,г. Могилев, пр. Мира, 43
Содержание
1 Основные определения и формулы 4
2 Обработка результатов прямых измерений 6
3 Обработка результатов косвенных измерений 11
4 Класс точности и нормирование погрешности 16
5 Определение погрешностей при различных законах
распределения 17
6 Аппроксимация функций распределения случайных
погрешностей 17
Список литературы 18
Приложения 19
Основные определения и формулы
Абсолютной погрешностью результата измерения D называют разность между результатом измерения хи и истинным значением измеряемой величины х.
. (1.1)
Истинное значение величины являе
тся идеализированной ее характеристикой. На практике может быть определено действительное значение величины, которое настолько приближается к истинному, что может быть использовано вместо него.
Погрешность D является случайной величиной и может быть представлена в виде
, (1.2)
где 
– систематическая погрешность;
– случайная погрешность.
Если значение Dc известно, то систематическую погрешность можно исключить, введя поправку, приняв за окончательный результат измерения хиспр. исправленный результат измерения.
. (1.3)
Исключить случайную погрешность нельзя, т.к. неизвестно, какое конкретно значение приняла случайная величина D при данном измерении. Для оценки влияния случайной погрешности на результат измерения задаются положительными значениями D1 и D2 и определяют вероятность того, что измеряемая величина х заключена между 
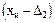и 
. Интервал 
называется доверительным интервалом, а вероятность того, что х находится внутри этого интервала – доверительной вероятностью Рд.
. (1.4)
Обычно принимают D1=D2. Тогда
. (1.5)
Если известен закон распределения погрешности D, т.е. плотность вероятности f(D), то
(1.6)
Числовые характеристики закона распределения f(D) – математическое ожидание Dc, дисперсия D и среднее квадратическое отклонение s - могут быть определены по формулам
; (1.7)
; (1.8)
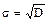, (1.9)
где D – дисперсия.
При нормальном законе распределения погрешностей
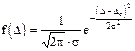. (1.10)
В этом случае, используя таблицу функций Лапласа Ф(z), можно определить
, (1.11)
причем 
.
Иногда закон распределения погрешностей неизвестен, однако известны его числовые характеристики Dc и s. Тогда для грубой оценки снизу доверительной вероятности Рд при заданном симметричном доверительном интервале D1 можно воспользоваться неравенством
, (1.12)
откуда
. (1.13)
