Удобной механической моделью решения вероятностных задач является схема урн (схема случаев). Урна представляет собой непрозрачную емкость («черный ящик») достаточного объема, в которую помещены одинаковые, симметричные тела − элементы данного множества (шары) в известном количестве. Испытание (эксперимент) состоит в извлечении шара из «черного ящика» при обеспечении следующих симметричных условий:
- одинаковая возможность извлечения любого шара (случайные события равновероятны),
- шары извлекаются последовательно, по одному. В результате испытания исключается совместное появление двух и более шаров или в результате испытания наступление одного случайного события исключает наступление другого (случайные события несовместны);
- в результате испытаний появление известного конечного множества шаров, загруженных в урну, исчерпывает собой все возможные исходы или появление хотя бы одного из случайных событий является достоверным (случайные события образуют полную группу).
Случайные события называются случаями (множество элементарных событий), если в процессе проведения эксперимента обеспечиваются сформулированные три условия симметрии − равновероятность, несовместность, полнота группы событий. Тогда классическая вероятность случайного события 
определяется как отношение числа элементарных исходов, благоприятствующих появлению события 
, к общему числу возможных элементарных исходов 
, т.е.
.
Пример: В ящике содержится 
деталей, среди которых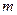 
качественных. Найти вероятность того, что наудачу извлеченная деталь является: а) качественной 
; б) дефектной 
.
Решение: Рассматриваемая задача удовлетворяет трем сформулированным условиям симметрии. Тогда, согласно классического определения вероятности, находим:
, 
.
Очевидно, что 
.
Число возможных и благоприятных элементарных событий вычисляется с помощью формул комбинаторики. Основные из этих формул выводятся ниже.
