ѕример: ѕусть в распор€жении конструктора имеетс€ четыре взаимозамен€емых блока (элемента): 
 . онструктивный узел состоит из трех блоков. “ребуетс€ найти множество конструктивных схем узла, отличающихс€ между собой как составом блоков, так и пор€дком их следовани€.
. онструктивный узел состоит из трех блоков. “ребуетс€ найти множество конструктивных схем узла, отличающихс€ между собой как составом блоков, так и пор€дком их следовани€.
”пор€доченные наборы, состо€щие из  элементов (подмножества), вз€тых из множества
элементов (подмножества), вз€тых из множества  элементов
элементов  , отличающиес€ хот€ бы одним элементом (составом) и пор€дком их следовани€ (расположением) называютс€ размещени€ми (Arrangement), а их количество обозначаетс€ в виде
, отличающиес€ хот€ бы одним элементом (составом) и пор€дком их следовани€ (расположением) называютс€ размещени€ми (Arrangement), а их количество обозначаетс€ в виде  − число размещений из
− число размещений из  элементов по
элементов по  . »скомые упор€доченные наборы − конструктивные схемы, удобно находить с помощью следующих цепных диаграмм
. »скомые упор€доченные наборы − конструктивные схемы, удобно находить с помощью следующих цепных диаграмм
 ќткуда непосредственно находитс€ искомое множество конструктивных схем узла и их количество
ќткуда непосредственно находитс€ искомое множество конструктивных схем узла и их количество  как число размещений из
как число размещений из  по
по  :
:

или

т.е.
 .
.
ћетодом математической индукции легко получить общую формулу
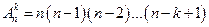 .
.
¬ частном случае, когда  , упор€доченные наборы (подмножества) отличаютс€ между собой лишь пор€дком следовани€ элементов − их расположением в наборе. —остав элементов в наборе − неизменен. “акие упор€доченные соединени€ элементов в группы называютс€ перестановками (Permutation) и их количество обозначаетс€ в виде
, упор€доченные наборы (подмножества) отличаютс€ между собой лишь пор€дком следовани€ элементов − их расположением в наборе. —остав элементов в наборе − неизменен. “акие упор€доченные соединени€ элементов в группы называютс€ перестановками (Permutation) и их количество обозначаетс€ в виде  − число перестановок из
− число перестановок из  элементов. ќчевидно, что
элементов. ќчевидно, что
 , или
, или  , т.е.
, т.е.  .
.
”пор€доченные наборы, состо€щие из  элементов, вз€тых из
элементов, вз€тых из  элементов
элементов  , отличающиес€ между собой лишь составом (хот€ бы одним элементом), а пор€док следовани€ элементов − произволен (несущественен), называютс€ сочетани€ми (Combination), а их количество обозначаетс€ в виде
, отличающиес€ между собой лишь составом (хот€ бы одним элементом), а пор€док следовани€ элементов − произволен (несущественен), называютс€ сочетани€ми (Combination), а их количество обозначаетс€ в виде  − число сочетаний из
− число сочетаний из  элементов по
элементов по  .
.
“ак как размещени€ включают перестановки и сочетани€, то очевидно
 .
.
ƒействительно, из приведенной диаграммы нетрудно найти группы элементов, образующих сочетани€ из четырех по три, т.е.  .
.

ѕроизвод€ перестановки трех элементов  в каждом из этих сочетаний
в каждом из этих сочетаний  , получим все размещени€
, получим все размещени€  , приведенные на диаграмме в виде матрицы состо€ний, где количество строк определ€етс€ числом перестановок, а количество столбцов − числом сочетаний:
, приведенные на диаграмме в виде матрицы состо€ний, где количество строк определ€етс€ числом перестановок, а количество столбцов − числом сочетаний:

т.е.  .
.
ќткуда следует формула дл€ числа сочетаний:

или в развернутом виде:
 .
.
”читыва€, что  , искомым формулам можно придать лаконичный вид:
, искомым формулам можно придать лаконичный вид:
 ,
,  .
.
ѕример: ¬ €щике  деталей, из них
деталей, из них 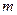 дефектных. Ќаудачу извлечены
дефектных. Ќаудачу извлечены
 деталей. Ќайти веро€тность того, что все извлеченные детали качественны.
деталей. Ќайти веро€тность того, что все извлеченные детали качественны.
–ешение: ќбщее число возможных элементарных исходов:  . „исло элементарных исходов, благопри€тствующих по€влению искомого случайного событи€
. „исло элементарных исходов, благопри€тствующих по€влению искомого случайного событи€  −
−  извлеченных деталей качественны:
извлеченных деталей качественны:  .
.
“огда
 .
.
ѕример: ¬ €щике находитс€ семь блоков, обозначенные  ,
,  ,
,  ,
, 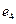 ,
,  ,
,  ,
,  , из которых в определенной очередности собираетс€ узел. »звестно, что блоки
, из которых в определенной очередности собираетс€ узел. »звестно, что блоки  и
и  , а также
, а также  и
и 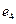 − взаимозамен€емые. — учетом взаимозамен€емости, номерам блоков присвоены буквы следующим образом:
− взаимозамен€емые. — учетом взаимозамен€емости, номерам блоков присвоены буквы следующим образом:  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . ”зел будет правильно функционировать (правильно собран), если блоки последовательно разместить в очередности, имеющей закодированное слово Ђбабушкаї. Ќайти веро€тность того, что наудачу извлеченные блоки расположатс€ в пор€дке, при котором узел будет собран правильно, т.е. в результате испытани€ составитс€ последовательность букв, имеющих смысл − Ђбабушкаї.
. ”зел будет правильно функционировать (правильно собран), если блоки последовательно разместить в очередности, имеющей закодированное слово Ђбабушкаї. Ќайти веро€тность того, что наудачу извлеченные блоки расположатс€ в пор€дке, при котором узел будет собран правильно, т.е. в результате испытани€ составитс€ последовательность букв, имеющих смысл − Ђбабушкаї.
|
|
|
–ешение: ќбщее число возможных элементарных исходов:  , т.е. 5040. исходы благопри€тствующих по€влению искомого слова следующие:
, т.е. 5040. исходы благопри€тствующих по€влению искомого слова следующие:

“аким образом
 .
.






